题目内容
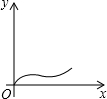
8.如图(1),在直角梯形ABCD中,AB∥DC,∠B=90°,动点P从点B出发,沿梯形的边由B→C→D→A运动,设点P运动的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图(2)所示,则△ABC的面积为16.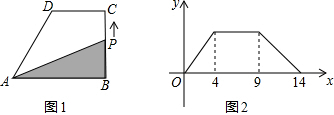
分析 由题意知:BC=4,DC=9-4=5,AD=5,过点D作DN⊥AB于点N,利用勾股定理求得AN,进一步求得AB,利用三角形的面积计算公式得出答案即可.
解答 解:根据图2可知当点P在CD上运动时,△ABP的面积不变,与△ABC面积相等;且不变的面积是在x=4,x=9之间;
所以在直角梯形ABCD中BC=4,CD=5,AD=5.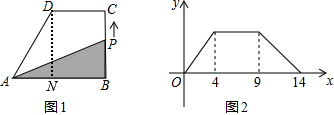
过点D作DN⊥AB于点N,则有DN=BC=4,BN=CD=5,
在Rt△ADN中,AN=$\sqrt{A{D}^{2}-D{N}^{2}}$=3,
所以AB=BN+AN=5+3=8
所以△ABC的面积为$\frac{1}{2}$AB•BC=$\frac{1}{2}$×8×4=16.
故答案为:16.
点评 本题考查了动点问题的函数图象,解决本题的关键是读懂图意,得到相应的直角梯形中各边之间的关系.此题考查了学生从图象中读取信息的数形结合能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
8.有四张分别画有线段、等边三角形、平行四边形和正方形的四个图形的卡片,它们的背面都相同,现将它们背面朝上,从中翻开任意一张的图形是中心对称图形,但不是轴对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
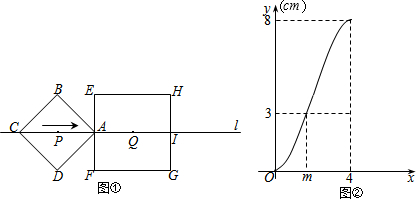
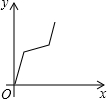
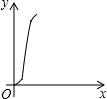
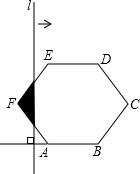 如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )
如图,在正六边形ABCDEF中,直线l⊥AB,直线l从点F开始向右作匀速平行移动,设直线l移动的时间为x,扫过正六边形ABCDEF的面积(图中阴影部分)为y,则下列各图中,能够反映y与x的函数关系的大致图象是( )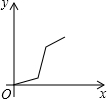
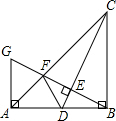 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①$\frac{AG}{AB}=\frac{FG}{FB}$;②FG=$\frac{1}{2}$FB;③AF=$\frac{\sqrt{2}}{3}AB$;④S△ABC=5S△BDF,其中正确结论的序号是①②③.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①$\frac{AG}{AB}=\frac{FG}{FB}$;②FG=$\frac{1}{2}$FB;③AF=$\frac{\sqrt{2}}{3}AB$;④S△ABC=5S△BDF,其中正确结论的序号是①②③.