题目内容
18.某工厂生产的某种产品按质量分为10个等级.第1级(最低级)产品每天能生产95件,每件利润6元.已知每提高一个级别,每件利润增加2元,但每天产量减少5件.(1)若生产第3级产品,则每天产量为85件,每件利润为10元;
(2)若生产第x级产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数解析式;
(3)若生产第x级的产品一天的总利润为1120元,求该产品的质量等级.
分析 (1)根据题意列算式计算即可;
(2)每件的利润为6+2(x-1),生产件数为95-5(x-1),则y=[6+2(x-1)][95-5(x-1)];
(3)由题意可令y=1120,求出x的实际值即可
解答 解:(1)每天产量95-5(3-1)=85,每件的利润为6+2×(3-1)=10,
故答案为:85,10;
(2)∵第一级的产品一天能生产95件,每件利润6元,每提高一个级别,每件利润加2元,但一天生产量减少5件.∴第x级别,提高的级别是(x-1)档.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10),
(3)由题意可得:-10x2+180x+400=1120,
整理得:x2-18x+72=0,
解得:x1=6,x2=12(舍去).
答:该产品的质量级别为第6级.
点评 本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
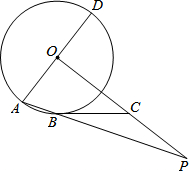 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.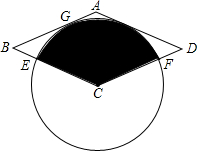 如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.
如图,以菱形ABCD的顶点C为圆心画⊙C,⊙C与AB相切于点G,与BC、CD分别相交于点E、F.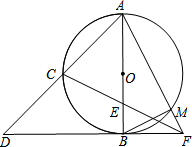 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.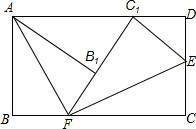 已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.
已知四边形ABCD是矩形,BF=1,FC=3,沿EF,AF折叠,点C落在C1处,点B落在FC1边上的B1,求AB=$\sqrt{5}$.