题目内容
17.有下列4个命题:①方程x2-($\sqrt{3}$+$\sqrt{2}$)x+$\sqrt{6}$=0的两个根是$\sqrt{3}$与$\sqrt{2}$;②点P(x,y)坐标x,y满足x2+y2+4x-2y+5=0,若P点在y=$\frac{k}{x}$上,则k=-2;③在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=4,BD=$\frac{9}{4}$,则CD=3;④若实数b,c满足1+b+c>0,1-b+c<0,则关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大根x0满足-1<x0<0.其中真命题的个数为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 利用因式分解法解方程可对①进行判断;利用配方法求出x、y的值,然后根据反比例函数图象上点的坐标特征对②进行判断;根据射影定理对③进行判断;根据抛物线与x轴的交点问题对④进行判断.
解答 解:方程x2-($\sqrt{3}$+$\sqrt{2}$)x+$\sqrt{6}$=0的两个根是$\sqrt{3}$与$\sqrt{2}$,所以①正确;
由x2+y2+4x-2y+5=0得(x+2)2+(y-1)2=0,则x=-2,y=1,所以k=-2×1=-2,所以②正确;
CD2=AD•BD=4×$\frac{9}{4}$,则CD=3,所以③正确;
抛物线y=x2+bx+c=0的开口向上,当x=1时,y=1+b+c>0,当x=-1时,y=1-b+c<0,即抛物线与x轴有两个交点,所以关于x的方程x2+bx+c=0一定有两个不相等的实数根,由于抛物线与x轴的一个交点可能在(0,0)与(1,0)之间,所以④错误.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
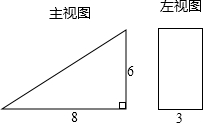 有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.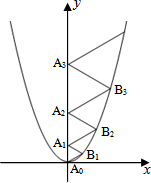 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008. 如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.
如图,在菱形ABCD中,DE⊥AB,sinA=$\frac{4}{5}$,BE=2,则tan∠BDE的值是$\frac{1}{2}$.