题目内容
7.已知代数式(mx2+2mx-1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.分析 先把代数式按照多项式乘以多项式展开,因为化简后是一个四次多项式,所以x的最高指数m+2=4;不含二次项,即二次项的系数为0,即可解答.
解答 解:(mx2+2mx-1)(xm+3nx+2)=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx-xm-3nx-2,
因为该多项式是四次多项式,
所以m+2=4,
解得:m=2,
原式=2x4+(6n+4)x3+(3+12n)x2+(8-3n)x-2
∵多项式不含二次项
∴3+12n=0,
解得:n=$-\frac{1}{4}$,
所以一次项系数8-3n=8.75.
点评 本题考查了多项式乘以多项式,解决本题的关键是明确化简后是一个四次多项式,所以x的最高指数m+2=4;不含二次项,即二次项的系数为0,即可解答.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
2.下列命题错误的是( )
| A. | 对角线相互平分的四边形是平行四边形 | |
| B. | 对角线相互平分且相等的四边形是矩形 | |
| C. | 对角线相互平分且垂直的四边形是菱形 | |
| D. | 对角线相等且垂直的四边形是正方形 |
12.已知直线y=kx+b,若k+b<0,kb>0,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在直角坐标系中,点P落在直线x-2y+6=0上,O为坐标原点,则|OP|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
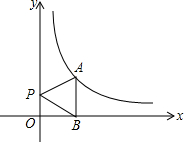 已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,
已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,