题目内容
平行四边形ABCD中,AC,BD交于点O,E为OB中点,AE延长线交BC于F,求证:CF=2BF.
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:由四边形ABCD是平行四边形,易得△BEF∽△DEA,然后由E为OB中点,根据相似三角形的对应边成比例,即可证得结论.
解答: 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴△BEF∽△DEA,
∴BF:AD=BE:DE,
∵E为OB中点,
∴BE:DE=1:3,
∴BF:AD=BF:BC=1:3,
∴BF:CF=1:2,
∴CF=2BF.
 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,OB=OD,
∴△BEF∽△DEA,
∴BF:AD=BE:DE,
∵E为OB中点,
∴BE:DE=1:3,
∴BF:AD=BF:BC=1:3,
∴BF:CF=1:2,
∴CF=2BF.
点评:此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 已知,如图:△ABC中,直线DF分别交BC、AD于D、E,交BA的延长线于点F,且
已知,如图:△ABC中,直线DF分别交BC、AD于D、E,交BA的延长线于点F,且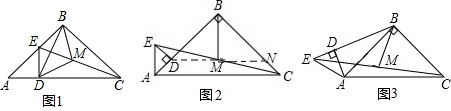
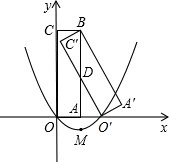 如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形.
如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形. 解不等式组
解不等式组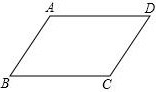 已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明)
已知:如图,在四边形ABCD中,AB∥CD,∠B=∠D.求证:AD∥BC(用两种不同的方法证明) 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短. 实数x在数轴上的位置如图所示,则化简
实数x在数轴上的位置如图所示,则化简