题目内容
19.先化简,再求值:$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$),其中x=$\sqrt{2}$-2.分析 先把括号内通分和除法运算化为乘法运算,再把分母因式分解,然后约分得到原式=$\frac{1}{x+3}$,最后把x的值代入计算即可.
解答 解:原式=$\frac{x-3}{x-2}$÷$\frac{(x+2)(x-2)-5}{x-2}$
=$\frac{x-3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$,
当x=$\sqrt{2}$-2时,原式=$\frac{1}{\sqrt{2}-2+3}$=$\sqrt{2}$-1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
17.方程组$\left\{\begin{array}{l}{x+y=2}\\{2x+2y=3}\end{array}\right.$没有解,因此直线y=-x+2和直线y=-x+$\frac{3}{2}$在同一平面直角坐标系中的位置关系是( )
| A. | 重合 | B. | 平行 | ||
| C. | 相交 | D. | 以上三种情况都有可能 |
18.直线y1=k1x+4与双曲线y2=$\frac{{k}_{2}}{x}$交于点(3,1),(m,3),则当y1>y2时,自变量x的范围是( )
| A. | 1<x<3 | B. | 0<x<1 | C. | x<0,1<x<3 | D. | 0<x<1,x>3 |
14. 如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
 如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )
如图,已知BD∥AC,∠1=65°,∠A=40°,则∠2的大小是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
11.要反映2015年末嘉兴市各个县(区)常住人口占嘉兴市总人口的比例,宜采用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数直方图 |
8.下列各值中是方程组$\left\{\begin{array}{l}a+b=3\\ a-b=1\end{array}$的解的是( )
| A. | $\left\{\begin{array}{l}a=1\\ b=2\end{array}$ | B. | $\left\{\begin{array}{l}a=2\\ b=1\end{array}$ | C. | $\left\{\begin{array}{l}a=3\\ b=1\end{array}$ | D. | $\left\{\begin{array}{l}a=4\\ b=5\end{array}$ |
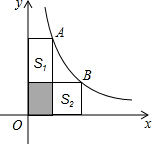 如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.
如图,点A、B在函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B分别向x、y轴作垂线.记矩形AEFP面积为S1,矩形BPCD面积为S2,阴影部分图形的面积恰好等于S1,则S1+S2=4.