题目内容
15.已知圆锥的侧面展开图是一个半圆,则母线与高的夹角是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
分析 设出圆锥的半径与母线长,利用圆锥的底面周长等于侧面展开图的弧长得到圆锥的半径与母线长,进而表示出母线与高的夹角的正弦值,也就求出了夹角的度数.
解答 解:设圆锥的母线长为R,底面半径为r,
则:πR=2πr,
∴R=2r,
∴母线与高的夹角的正弦值=$\frac{r}{R}$=$\frac{1}{2}$,
∴母线与高的夹角是30°.
故选:B.
点评 此题主要考查了圆锥的计算,本题用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;注意利用一个角相应的三角函数值求得角的度数.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | 2x2+x2=3x4 | B. | (-mn2)•(2mn)=-2m2n3 | C. | y8÷y2=y4 | D. | (3a2b)2=6a4b2 |
6.在同一平面内,a、b、c是直线,下列说法正确的是( )
| A. | 若a∥b,b∥c 则 a∥c | B. | 若a⊥b,b⊥c,则a⊥c | ||
| C. | 若a∥b,b⊥c,则a∥c | D. | 若a∥b,b∥c,则a⊥c |
10.一个多边形的每一个外角都是45°,那么这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十二边形 |
7. 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CDE | D. | ∠C+∠CDA=180° |
4.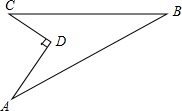 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )| A. | 60米2 | B. | 48米2 | C. | 30米2 | D. | 24米2 |