题目内容
15.先化简$\frac{{{x^2}-4}}{{{x^2}-9}}÷(1+\frac{1}{x-3})$,再从不等式2x-3<7的正整数解中选一个合适的数代入原式求值.分析 先根据分式混合运算的法则把原式进行化简,再求出不等式的解集,选出合适的x的值代入进行计算即可;
解答 解:原式=$\frac{(x+2)(x-2)}{(x+3)(x-3)}$÷$\frac{x-2}{x-3}$
=$\frac{(x+2)(x-2)}{(x+3)(x-3)}$•$\frac{x-3}{x-2}$
=$\frac{x+2}{x+3}$,
解不等式得x<5,但是x≠2,且x≠3.
当x=4时,原式=$\frac{6}{7}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
6.若x+y=5,x-y=3,则x2-y2的值是( )
| A. | 8 | B. | 15 | C. | 2 | D. | 4 |
5.下列说法正确的是( )
| A. | |-3|=-3 | B. | 0的倒数是0 | C. | 9的平方根是3 | D. | -4的相反数是4 |
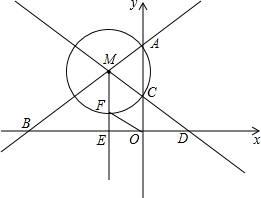 如图,直线y=$\frac{3}{4}$x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
如图,直线y=$\frac{3}{4}$x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF. 如图,∠F的内错角有∠AEF和∠ADF.
如图,∠F的内错角有∠AEF和∠ADF.