题目内容
9.已知抛物线C:y=x2-4x.(1)求抛物线C的开口方向、对称轴和顶点坐标;
(2)将抛物线C向下平移,得抛物线C′,使抛物线C′的顶点落在直线y=-x-7上.
①求抛物线C′的解析式;
②抛物线C′与x轴的交点为A,B(点A在点B的左侧),抛物线C′的对称轴于x轴的交点为N,点M是线段AN上的一点,过点M作直线MF⊥x轴,交抛物线C′于点F,点F关于抛物线对称轴的对称点为D,点P是线段MF上一点,且MP=$\frac{1}{4}$MF,连接PD,作PE⊥PD交x轴于点E,且PE=PD,求点E的坐标.
分析 (1)把抛物线解析式化为顶点式可求得抛物线C的开口方向、对称轴和顶点坐标;
(2)①可设平移后的抛物线解析式为y=x2-4x-m,可求得其顶点坐标,代入直线y=-x-7,可求得m的值,则可求得抛物线C′的解析式;②连接FD,由条件可证明△EPM≌△PDF,可求得PM=DF,EM=PF,设出F点坐标,则可分别表示出PM和DF的长,由条件可得到关于点F坐标的方程,可求得M、F的坐标,则可出E点坐标.
解答 解:
(1)∵y=x2-4x=(x-2)2-4,
∴抛物线开口向上,对称轴为x=2,顶点坐标为(2,-4);
(2)①设抛物线C′的解析式为y=(x-2)2-4-m,
则抛物线C′的顶点坐标为(2,-4-m),
∵抛物线C′的顶点落在直线y=-x-7上,
∴-4-m=-2-7,解得m=5;
②如图,连接FD,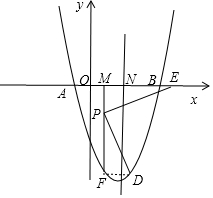
由①可得抛物线C′的解析式为y=x2-4x-5,
令y=0可得x2-4x-5=0,解得x=-1或x=5,
∵点A在点B的左侧,
∴A(-1,0),B(5,0),
∵点F关于抛物线对称轴对称点为D,且MF⊥x轴,
∴DF⊥MF,
∴∠EMP=∠PFD=90°,
∵PE⊥PD,
∴∠EPD+∠MPE=∠EPD+∠D=90°,
∴∠MPE=∠D,
在△EPM和△PDF中
$\left\{\begin{array}{l}{∠MPE=∠D}\\{∠EMP=∠PFD}\\{PE=PD}\end{array}\right.$
∴△EPM≌△PDF(AAS),
∴PM=DF,EM=PF,
设点F坐标为(t,t2-4t-5),
∵点M在线段AN上,
∴-1<t<2,
∴DF=2(2-t),PM=-$\frac{1}{4}$(t2-4t-5),
∵PM=DF,
∴2(2-t)=-$\frac{1}{4}$(t2-4t-5),解得t=1或t=11(不合题意,舍去),
∴M(1,0),F(1,-8),
∴MF=8,MP=2,
∴PF=8-2=6,
∴EM=PF=6,
∴OE=OM+ME=7,
∴E点坐标为(7,0).
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、图象的平移、全等三角形的判定和性质及方程思想等知识.在(1)中把抛物线解析式化为顶点式是解题的关键,在(2)①中求得平移后的抛物线的顶点坐标是解题的关键,在(2)②中构造全等三角形,用F点的坐标表示出PM和DF的长是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 2x+3x=9+5 | B. | 2x-3x=9+5 | C. | 2x-3x=-9+5 | D. | 2x-3x=9-5 |
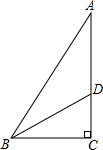 如图,在 Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若CD=3cm,则点D到AB的距离是3cm..
如图,在 Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若CD=3cm,则点D到AB的距离是3cm.. (1)解方程组$\left\{\begin{array}{l}x+2y=5\\ x+y=2.\end{array}$
(1)解方程组$\left\{\begin{array}{l}x+2y=5\\ x+y=2.\end{array}$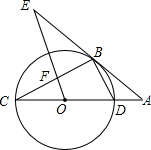 如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.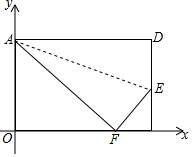 折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).
折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).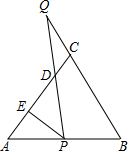 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则:①PD=DQ;②∠Q=30°;③DE=$\frac{1}{2}$AC;④AE=$\frac{1}{2}$CQ.其中正确的结论是①③④.(把所有正确结论的序号都写在横线上).
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则:①PD=DQ;②∠Q=30°;③DE=$\frac{1}{2}$AC;④AE=$\frac{1}{2}$CQ.其中正确的结论是①③④.(把所有正确结论的序号都写在横线上).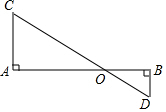 如图,已知AC⊥AB,BD⊥AB,AO=5cm,BO=3cm,OC=10cm.求OD和CD.
如图,已知AC⊥AB,BD⊥AB,AO=5cm,BO=3cm,OC=10cm.求OD和CD.