题目内容
4.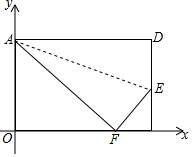 折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).
折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).
分析 首先求出BF的长度;然后运用EF=DE(设为λ),列出关于λ的方程,求出λ即可解决问题.
解答 解:如图,∵四边形ABCD为矩形,
∴AD=BC=10,DC=AB=8;
由勾股定理得:BF=$\sqrt{1{0}^{2}-{8}^{2}}$=6;CF=10-6=4,
由题意得:EF=DE(设为λ),
则EC=8-λ;由勾股定理得:λ2=42+(8-λ)2,
解得:λ=5,
∴EC=8-5=3,
∴点F和点E坐标分别为F(6,0)、E(10,3);
故答案为:(6,0)、(10,3).
点评 该题考查了翻折变换的性质、勾股定理及其应用问题;灵活运用翻折变换的性质、勾股定理是解题的关键.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | a6÷a2=a3 | B. | a5-a2=a3 | ||
| C. | (3a3)2=6a9 | D. | 2(a3b)2-3(a3b)2=-a6b2 |
8.在数轴上,与表示数-1的点的距离是3的点表示的数是( )
| A. | 2 | B. | 2或-4 | C. | -4 | D. | ±3 |
 由5个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )
由5个相同的小立方体搭成的几何体如图所示,则从正面看到的几何体的形状是( )



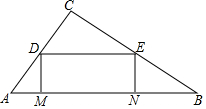 如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).
如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).