题目内容
8. 如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是( )
如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是( )| A. | 9 | B. | 18 | C. | 27 | D. | 36 |
分析 由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,又因为△AOB的周长为15,AB=6,所以OA+OB=13,所以AC+BD=2OA+2OB=2(OA+OB)=18.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,
∵△AOB的周长为15,AB=6,
∴AB+OA+OB=15,
∴OA+OB=9,
∴AC+BD=2OA+2OB=2(OA+OB)=18.
故选B.
点评 此题考查了平行四边形的性质:平行四边形的对角线互相平分.解题的关键是注意整体思想的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
18.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{3}}$ |
19.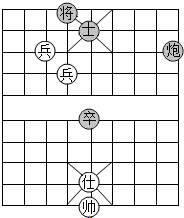 如图是中国象棋的一盘残局,如果用(2,-3)表示“帅”的位置,用(6,4)表示的“炮”位置,那么“将”的位置应表示为( )
如图是中国象棋的一盘残局,如果用(2,-3)表示“帅”的位置,用(6,4)表示的“炮”位置,那么“将”的位置应表示为( )
 如图是中国象棋的一盘残局,如果用(2,-3)表示“帅”的位置,用(6,4)表示的“炮”位置,那么“将”的位置应表示为( )
如图是中国象棋的一盘残局,如果用(2,-3)表示“帅”的位置,用(6,4)表示的“炮”位置,那么“将”的位置应表示为( )| A. | (6,4) | B. | (4,6) | C. | (1,6) | D. | (6,1) |
17.若一组数据0,2,-1,4,x的中位数为0,则在下列数值中x的可能值是( )
| A. | -3 | B. | 6 | C. | -2 | D. | -2或-3 |
 如图,正五边形ABCDE内接于⊙O,则∠ABD=72°.
如图,正五边形ABCDE内接于⊙O,则∠ABD=72°.