题目内容
10.观察各数:$\frac{1}{2}$$\sqrt{27}$,3$\sqrt{\frac{1}{3}}$,2$\sqrt{3}$,$\frac{1}{2}$$\sqrt{75}$.其中最小数与最大数的和为$\frac{7\sqrt{3}}{2}$(结论化简).分析 直接化简二次根式,进而找出最大和最小的值计算得出答案.
解答 解:$\frac{1}{2}$$\sqrt{27}$=$\frac{3}{2}$$\sqrt{3}$,3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$,2$\sqrt{3}$,$\frac{1}{2}$$\sqrt{75}$=$\frac{5}{2}$$\sqrt{3}$,
∴$\frac{1}{2}$$\sqrt{75}$=$\frac{5}{2}$$\sqrt{3}$,最大,3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$,最小,
故最小数与最大数的和为:$\frac{5\sqrt{3}}{2}$+$\sqrt{3}$=$\frac{7\sqrt{3}}{2}$.
故答案为:$\frac{7\sqrt{3}}{2}$.
点评 此题主要考查了实数比较大小,正确化简二次根式是解题关键.

练习册系列答案
相关题目
15.3:8的前项乘以3,要使比值不变,后项应该( )
| A. | 加上6 | B. | 乘以16 | C. | 减去6 | D. | 乘以3 |
19.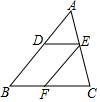 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
 已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
已知在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{BF}{FC}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |