题目内容
6.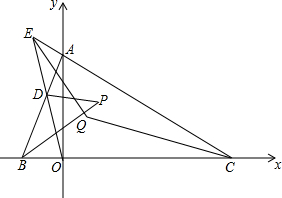 在直角坐标系中,已知△ABC的三个顶点是A(0,a)、B(b,0)、C(c,0),D是线段AB上任一点,直线OD交直线AC于E,∠ADO和∠ABO的平分线交于点P,若E点在AC边的延长线上,∠ACB与∠AED的平分线交于Q点,下面两个结论:
在直角坐标系中,已知△ABC的三个顶点是A(0,a)、B(b,0)、C(c,0),D是线段AB上任一点,直线OD交直线AC于E,∠ADO和∠ABO的平分线交于点P,若E点在AC边的延长线上,∠ACB与∠AED的平分线交于Q点,下面两个结论:①∠P+∠Q的值不变;
②∠P-∠Q的值不变;
其中只有一个结论是正确的,请选择正确的结论并给出证明,求出定值.
分析 由∠ADO和∠ABO的平分线交于点P,得到∠ADP=$\frac{1}{2}∠$ADO=∠ABP+∠P,∠ABP=$\frac{1}{2}∠$ABO,根据三角形外角的性质得到$\frac{1}{2}$∠ADO=$\frac{1}{2}∠$ABO+$\frac{1}{2}∠$BOE=$\frac{1}{2}∠$ABO+∠P,于是得到∠P=$\frac{1}{2}∠$BOE,由∠ACB与∠AED的平分线交于Q点,得到∠CEQ+∠ECQ=$\frac{1}{2}$(∠OEC+∠OCE),由外角的性质得到∠BOE=∠OCE+∠OEC,于是得到∠CEQ+∠ECQ=$\frac{1}{2}$∠BOE,然后等量代换得到结论.
解答 解:①∠P+∠Q的值不变;
理由:∵∠ADO和∠ABO的平分线交于点P,
∴∠ADP=$\frac{1}{2}∠$ADO=∠ABP+∠P,∠ABP=$\frac{1}{2}∠$ABO,
∵∠ADO=∠ABO+∠BOE,
∴$\frac{1}{2}$∠ADO=$\frac{1}{2}∠$ABO+$\frac{1}{2}∠$BOE=$\frac{1}{2}∠$ABO+∠P,
∴∠P=$\frac{1}{2}∠$BOE,
∵∠ACB与∠AED的平分线交于Q点,
∴∠CEQ+∠ECQ=$\frac{1}{2}$(∠OEC+∠OCE),
∵∠BOE=∠OCE+∠OEC,
∴∠CEQ+∠ECQ=$\frac{1}{2}$∠BOE,
∴∠P=∠CEQ+∠ECQ,
∵∠Q+∠CEQ+∠ECQ=180°,
∴∠P+∠Q=180°,
∴∠P+∠Q的值不变.
点评 本题考查了三角形的内角和,角平分线的定义,三角形外角的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
14.下列各组线段:①1cm、2cm、3cm; ②3cm、4cm、5cm;③3cm、5cm、8cm;④4cm、4cm、2cm;⑤6cm、14cm、5cm;其中能组成三角形的有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
15.下列说法中,正确的是( )
| A. | 单项式-$\frac{2{x}^{2}y}{5}$的系数是-2,次数是3 | |
| B. | 单项式a的系数为0,次数是3 | |
| C. | 24ab2c的系数是2,次数为8 | |
| D. | 一个n次多项式(n为正整数),它的每一项的次数都不大于n |