题目内容
 如图,菱形ABCD中,∠B=60°,以AC为边长的正方形ACEF的面积为3,则菱形ABCD的面积为( )
如图,菱形ABCD中,∠B=60°,以AC为边长的正方形ACEF的面积为3,则菱形ABCD的面积为( )| A、3 | ||||
B、
| ||||
C、3
| ||||
D、
|
考点:菱形的性质
专题:
分析:首先过点A作AH⊥BC于点H,由以AC为边长的正方形ACEF的面积为3,可求得AC=
,又由菱形ABCD中,∠B=60°,易得△ABC是等边三角形,继而求得高AH的长,则可求得答案.
| 3 |
解答: 解:过点A作AH⊥BC于点H,
解:过点A作AH⊥BC于点H,
∵以AC为边长的正方形ACEF的面积为3,
∴AC=
,
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=
,
∴AH=AB•sin∠B=
×
=
,
∴菱形ABCD的面积为:BC•AH=
×
=
.
故选B.
 解:过点A作AH⊥BC于点H,
解:过点A作AH⊥BC于点H,∵以AC为边长的正方形ACEF的面积为3,
∴AC=
| 3 |
∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=
| 3 |
∴AH=AB•sin∠B=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴菱形ABCD的面积为:BC•AH=
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
故选B.
点评:此题考查了菱形的性质、正方形的性质以及等边三角形的判定与性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
在平面直角坐标系中,点P(6,-5)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 在动画片(喜羊羊与灰太狼)中,有一次灰太狼追赶懒羊羊,在距离羊村60米处的地方上追上了懒羊羊,如图反映了这一过程,其中a表示与羊村的距离,t表示时间.根据相关信息,以下说法错误的是( )
在动画片(喜羊羊与灰太狼)中,有一次灰太狼追赶懒羊羊,在距离羊村60米处的地方上追上了懒羊羊,如图反映了这一过程,其中a表示与羊村的距离,t表示时间.根据相关信息,以下说法错误的是( )| A、一开始懒羊羊与灰太狼之间的距离是30米 |
| B、15秒后灰太狼追上了懒羊羊 |
| C、灰太狼跑了60米追上懒羊羊 |
| D、灰太狼追上懒羊羊时,懒羊羊跑了60米 |
计算(-6ab)2•(3a2b)的结果是( )
| A、18a4b3 |
| B、-36a4b3 |
| C、-108a4b3 |
| D、108a4b3 |
用配方法解方程x2-x-1=0,变形结果正确的是( )
| A、(x-1)2=2 | ||||
| B、(x-1)2=0 | ||||
C、(x-
| ||||
D、(x-
|
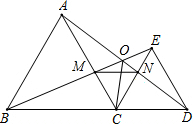 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论:
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论: