题目内容
关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )
A、k>
| ||
B、k≥
| ||
C、k≥
| ||
D、k>
|
考点:根的判别式,一元二次方程的定义
专题:
分析:根据判别式的意义得到△=(2k+1)2-4(k-2)2>0,然后解不等式即可.
解答:解:∵关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,
∴b2-4ac=(2k+1)2-4(k-2)2>0,且(k-2)2≠0
解得k>
,且k≠2
故选:D.
∴b2-4ac=(2k+1)2-4(k-2)2>0,且(k-2)2≠0
解得k>
| 3 |
| 4 |
故选:D.
点评:此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;以及一元二次方程的意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在动画片(喜羊羊与灰太狼)中,有一次灰太狼追赶懒羊羊,在距离羊村60米处的地方上追上了懒羊羊,如图反映了这一过程,其中a表示与羊村的距离,t表示时间.根据相关信息,以下说法错误的是( )
在动画片(喜羊羊与灰太狼)中,有一次灰太狼追赶懒羊羊,在距离羊村60米处的地方上追上了懒羊羊,如图反映了这一过程,其中a表示与羊村的距离,t表示时间.根据相关信息,以下说法错误的是( )| A、一开始懒羊羊与灰太狼之间的距离是30米 |
| B、15秒后灰太狼追上了懒羊羊 |
| C、灰太狼跑了60米追上懒羊羊 |
| D、灰太狼追上懒羊羊时,懒羊羊跑了60米 |
用配方法解方程x2-x-1=0,变形结果正确的是( )
| A、(x-1)2=2 | ||||
| B、(x-1)2=0 | ||||
C、(x-
| ||||
D、(x-
|
若∠A与∠B的两边分别平行,∠A=50°,则∠B=( )
| A、40° |
| B、50° |
| C、40°或140° |
| D、50°或130° |
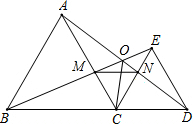 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论:
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连接OC、MN,则下列结论: