题目内容
(1)计算:(2015-π)0+|3-
|-
+(
)-1;
(2)已知:x=2+
,y=2-
,求代数式x2+3xy+y2的值;
(3)解方程组
.
| 12 |
| 6 | ||
|
| 1 |
| 3 |
(2)已知:x=2+
| 3 |
| 3 |
(3)解方程组
|
考点:二次根式的混合运算,零指数幂,负整数指数幂,解二元一次方程组
专题:计算题
分析:(1)根据零指数幂和负整数指数幂得到原式=1+2
-3-2
+3,然后合并即可;
(2)先计算出x+y=4,xy=1,再变形得到原式=(x+y)2+xy,然后利用整体代入的方法计算;
(3)利用加减消元法解方程组.
| 3 |
| 3 |
(2)先计算出x+y=4,xy=1,再变形得到原式=(x+y)2+xy,然后利用整体代入的方法计算;
(3)利用加减消元法解方程组.
解答:解:(1)原式=1+2
-3-2
+3
=1;
(2)∵x=2+
,y=2-
,
∴x+y=4,xy=1,
∴原式=(x+y)2+xy
=42+1
=17;
(3)方程组化简为
,
①×9-②得63y-3y=30,
解得y=
,
把y=
代入①得x+
=5,
解得x=
所以方程组的解为
.
| 3 |
| 3 |
=1;
(2)∵x=2+
| 3 |
| 3 |
∴x+y=4,xy=1,
∴原式=(x+y)2+xy
=42+1
=17;
(3)方程组化简为
|
①×9-②得63y-3y=30,
解得y=
| 1 |
| 2 |
把y=
| 1 |
| 2 |
| 7 |
| 2 |
解得x=
| 3 |
| 2 |
所以方程组的解为
|
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂、解二元一次方程组.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
如果a的相反数是6,那么a等于( )
| A、6 | ||
B、
| ||
C、-
| ||
| D、-6 |
2015的相反数是( )
A、-
| ||
| B、2015 | ||
C、
| ||
| D、-2015 |
 如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )
如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=( )| A、80° | B、50° |
| C、40° | D、20° |
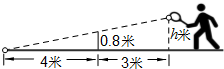 如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为
如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为