题目内容
3.计算:(1)$\sqrt{18}$+$\sqrt{32}$-$\sqrt{8}$
(2)6$\sqrt{\frac{x}{4}}$-$\sqrt{36x}$.
分析 (1)先根据二次根式的性质化简,再合并同类二次根式即可;
(2)先根据二次根式的性质化简,再合并同类二次根式即可.
解答 解:(1)$\sqrt{18}$+$\sqrt{32}$-$\sqrt{8}$
=3$\sqrt{2}$+4$\sqrt{2}$-2$\sqrt{2}$
=5$\sqrt{2}$;
(2)6$\sqrt{\frac{x}{4}}$-$\sqrt{36x}$
=3$\sqrt{x}$-6$\sqrt{x}$
=-3$\sqrt{x}$.
点评 本题考查的是二次根式的加减运算,掌握二次根式的性质、二次根式的加减法法则是解题的关键.

练习册系列答案
相关题目
13.已知整式x2-2x的值为6,则代数式5-2x2+4x的值为( )
| A. | 8 | B. | -7 | C. | 11 | D. | -17 |
14.把分式$\frac{2x+3y}{{x}^{2}-{y}^{2}}$的x、y均扩大为原来的10倍后,则分式的值( )
| A. | 为原分式值的$\frac{1}{10}$ | B. | 为原分式值的$\frac{1}{100}$ | ||
| C. | 为原分式值的10倍 | D. | 不变 |
18.若关于x的一元二次方程x2-x+a=0有实根,则a的值可以是( )
| A. | 2 | B. | 1 | C. | 0.5 | D. | 0 |
8.如图,从边长为(a+4)的正方形中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的周长为( )
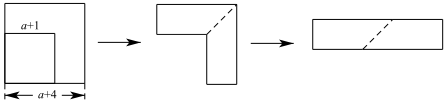

| A. | 4a+10 | B. | 4a+11 | C. | 4a+16 | D. | 以上答案都不对 |
13.下列调查中,调查方式选择正确的是( )
| A. | 了解100个灯泡的使用寿命,选择全面调查 | |
| B. | 了解某公园全年的游客流量,选择抽样调查 | |
| C. | 了解生产的50枚炮弹的杀伤半径,选择全面调查 | |
| D. | 了解一批袋装食品是否含有防腐剂,选择全面调查 |
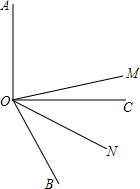 已知:如图,OM平分∠AOB,ON平分∠BOC.
已知:如图,OM平分∠AOB,ON平分∠BOC.