题目内容
7. 如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是①②④(请填序号)
如图,点P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC,PF⊥CD,垂足分别为点E、F,连接EF,下列结论①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP,其中正确的结论是①②④(请填序号)
分析 用正方形的性质和垂直的定义判断出四边形PECF是矩形,从而判定②正确;直接用正方形的性质和垂直得出①正确,利用全等三角形和矩形的性质得出④正确,由点P是正方形对角线上任意一点,说明AD和PD不一定相等,得出③错误.
解答 解:如图,
∵P为正方形ABCD的对角线BD上任一点,
∴PA=PC,∠C=90°,
∵过点P作PE⊥BC于点E,PF⊥CD,
∴∠PEC=∠DFP=∠PFC=∠C=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴PA=EF,故②正确,
∵BD是正方形ABCD的对角线,
∴∠ABD=∠BDC=∠DBC=45°,
∵∠PFC=∠C=90°,
∴PF∥BC,
∴∠DPF=45°,
∵∠DFP=90°,
∴△FPD是等腰直角三角形,故①正确,
在△PAB和△PCB中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$,
∴△PAB≌△PCB,
∴∠BAP=∠BCP,
在矩形PECF中,∠PFE=∠FPC=∠BCP,
∴∠PFE=∠BAP.故④正确,
∵点P是正方形对角线BD上任意一点,
∴AD不一定等于PD,
只有∠BAP=22.5°时,AD=PD,故③错误,
故答案为:①②④.
点评 此题主要考查了正方形的性质,矩形的判定和性质,全等三角形的判定和性质,垂直的定义,解本题的关键是判断出四边形PECF是矩形.

练习册系列答案
相关题目
7.$\frac{1}{4}$的相反数等于( )
| A. | $-\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{4}$ | D. | ±$\frac{1}{4}$ |
8.下列各数中,比-2小1的数是( )
| A. | -1 | B. | -3 | C. | 3 | D. | 1 |
15.圣诞节将至,小华决定购买一些贺卡,贺卡店有一则广告如图:
(1)如果小华只买15张,则购买贺卡共花去多少元钱?
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?
| 购买贺卡须知 (a)若购买20张以内(含20张),每张贺卡20元; (b)若购买20张以上,所购贺卡按照价格全部打七五折. |
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?
17.已知一个三角形的两边长分别是2和6,第三边为偶数,则此三角形的周长是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 13或15 |
 填空并完成以下推理:
填空并完成以下推理: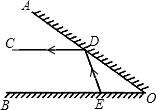 如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,光线经过镜子反射时,∠ADC=∠ODE,∠DEB=70°.
如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,光线经过镜子反射时,∠ADC=∠ODE,∠DEB=70°.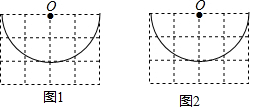 如图,在边长为1的正方形网格中画有一个圆心为O的半圆,请按要求准确作图.
如图,在边长为1的正方形网格中画有一个圆心为O的半圆,请按要求准确作图.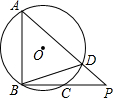 如图,点A,B,C,D在⊙O上,$\widehat{AB}$=2$\widehat{BC}$,$\widehat{AD}$=3$\widehat{BC}$,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为54°.
如图,点A,B,C,D在⊙O上,$\widehat{AB}$=2$\widehat{BC}$,$\widehat{AD}$=3$\widehat{BC}$,延长BC,AD交于点P,若∠CBD=18°,则∠P的大小为54°.