题目内容
2.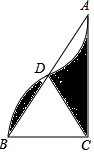 如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为4$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为4$\sqrt{3}$.
分析 阴影部分的面积=$\frac{1}{2}$三角形的面积,根据面积公式计算即可.
解答 解:解:由旋转可知AD=BD,
∵∠ACB=90°,AC=4$\sqrt{3}$,
∴CD=BD,
∵CB=CD,
∴△BCD是等边三角形,
∴∠BCD=∠CBD=60°,
∴BC=$\frac{\sqrt{3}}{3}$AC=4,
∴阴影部分的面积=$\frac{1}{2}$×4$\sqrt{3}$×4÷2=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 本题考查了三角形和扇形的面积公式及三角函数值,关键是得到△BCD是等边三角形.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12. 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
 如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )
如图,直线a∥b,∠1=30°,∠2=40°,且AD=AC,则∠3的度数是( )| A. | 70° | B. | 40° | C. | 45° | D. | 35° |
17. 如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )
如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )
 如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )
如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
 (1)计算:(a+b)2-b(2a+b)
(1)计算:(a+b)2-b(2a+b) 如图,每个小方格都是边长为1的小正方形.
如图,每个小方格都是边长为1的小正方形.