题目内容
10．化简分式：$\frac{a-1}{{a}^{2}-2a+1}$+$\frac{1}{a-1}$，并选取一个你喜欢的值代入求值．分析 先化成最简分式，再算加法，最后取符合条件的值代入求出即可．
解答 解：$\frac{a-1}{{a}^{2}-2a+1}$+$\frac{1}{a-1}$
=$\frac{a-1}{（a-1）^{2}}$+$\frac{1}{a-1}$
=$\frac{1}{a-1}$+$\frac{1}{a-1}$
=$\frac{2}{a-1}$，
∵根据已知算式a不能取1，
∴取a=2，
代入得：原式=$\frac{2}{2-1}$=2．
点评 本题考查了分式的混合运算和求值的应用，能求出原式=$\frac{2}{a-1}$是解此题的关键，此题是一道中档题目，难度适中，注意运算顺序．
练习册系列答案
阅读快车系列答案
相关题目
20．
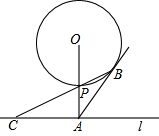如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，则⊙O的半径的最小值为（ ）
如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，则⊙O的半径的最小值为（ ）| A． | $\frac{5}{2}$ | B． | 2 | C． | $\sqrt{5}$ | D． | $\frac{5\sqrt{3}}{3}$ |
雾霾成为“两会”最大的民生话题． 浙江2015年十件民生实事已公布，雾霾治理居首位，杭州市确定了7600亿元的巨额治理投资，将用市场手段治理雾霾．7600亿元，用科学记数法表示为7.6×1011元．
19．
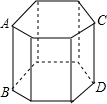如图，直六棱柱的底面是边长为4cm的正六边形，AB为8cm，则此直六棱柱左视图的面积为（ ）
如图，直六棱柱的底面是边长为4cm的正六边形，AB为8cm，则此直六棱柱左视图的面积为（ ）| A． | 32$\sqrt{3}$cm2 | B． | 32cm2 | C． | 64cm2 | D． | 16$\sqrt{3}$cm2 |