题目内容
 如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,则△ABC的周长为
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,则△ABC的周长为考点:线段垂直平分线的性质
专题:
分析:由线段垂直平分线的性质可得AE=EC,AD=CD,结合条件可求得AB+BC+AC=AB+BD+AD+2AE,代入可求得答案.
解答:解:
∵DE是AC的垂直平分线,
∴DA=CD,AE=EC,
∵△ABD的周长为16cm,
∴AB+BD+AD=16cm,
∴AB+BC+AC=AB+BD+DC+2AE=AB+BD+AD+2AE=16+8=24(cm),
即△ABC的周长为24cm,
故答案为:24cm.
∵DE是AC的垂直平分线,
∴DA=CD,AE=EC,
∵△ABD的周长为16cm,
∴AB+BD+AD=16cm,
∴AB+BC+AC=AB+BD+DC+2AE=AB+BD+AD+2AE=16+8=24(cm),
即△ABC的周长为24cm,
故答案为:24cm.
点评:本题主要考查线段垂直平分线的性质,利用线段垂直平分线上的点到线段两端点的距离相等把△ABC的周长转化成△ABD的周长与2AE的和是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4cm,BD的长度为( )
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4cm,BD的长度为( )| A、2cm | B、1.5cm |
| C、1cm | D、无法确定 |
现要做一个直角三角形的木架,以下四组木棒中,符合条件的是( )
| A、10cm,6cm,4cm |
| B、8cm,12cm,15cm |
| C、12cm,15cm,17cm |
| D、15cm,17cm,8cm |
计算(-
)-3的正确结果是( )
| 1 |
| a |
| A、a3 | ||
| B、-a3 | ||
C、
| ||
D、-
|
下列各组中的两项,不是同类项的是( )
| A、a2b与ab2 |
| B、-x2y与2yx2 |
| C、2πr与2r |
| D、35与53 |
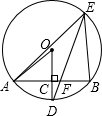 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.