题目内容
19.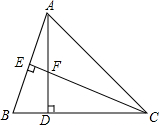 已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.
已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.
分析 根据已知条件得到∠ADC=∠ADB=∠BEC=90°,由余角的性质得到∠BAD=∠DCF,推出△ABD≌△CDF,得到AB=CF,等量代换得到AE=$\frac{1}{2}$AB,然后根据等腰三角形的性质得到结论.
解答 证明:∵AD⊥BC,CE⊥AB,
∴∠ADC=∠ADB=∠BEC=90°,
∴∠DCF+∠B=∠BAD+∠B=90°,
∴∠BAD=∠DCF,
在△ABD与△CDF中,
$\left\{\begin{array}{l}{∠ADB=∠CDF}\\{AD=CD}\\{∠BAD=∠DCF}\end{array}\right.$,
∴△ABD≌△CDF,
∴AB=CF,
∵AE=$\frac{1}{2}$CF,
∴AE=$\frac{1}{2}$AB,
∴AC=BC,
∴CE平分∠ACB.
点评 本题考查了全等三角形的判定和性质,垂直的定义,线段的垂直平分线的性质,等腰三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
17.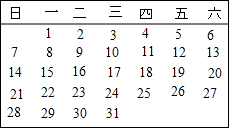 如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
 如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )| A. | 18 | B. | 33 | C. | 38 | D. | 81 |
 如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.
如图,BD是△ABC的角平分线,∠A=40°,∠ABC=70°,DF⊥BC于F,E为BC延长线上一点,CE=CD,求证:BF=EF.