题目内容
15.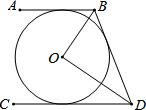 如图,AB、CD、BD都与⊙O相切,AB∥CD,OB=2,OD=3,则BD=$\sqrt{13}$.
如图,AB、CD、BD都与⊙O相切,AB∥CD,OB=2,OD=3,则BD=$\sqrt{13}$.
分析 根据切线长定理得到OB平分∠ABD,OD平分∠BDC,即∠OBD=$\frac{1}{2}$∠ABD,∠ODB=$\frac{1}{2}$∠BDC,再由平行线的性质得∠ABD+∠BDC=180°,所以∠OBD+∠ODB=90°,于是可判断△OBD为直角三角形,然后根据勾股定理可计算出BD.
解答 解:∵AB、CD、BD都与⊙O相切,
∴OB平分∠ABD,OD平分∠BDC,
∴∠OBD=$\frac{1}{2}$∠ABD,∠ODB=$\frac{1}{2}$∠BDC,
∵AB∥CD,
∴∠ABD+∠BDC=180°,
∴∠OBD+∠ODB=$\frac{1}{2}$×180°=90°,
∴∠BOD=90°,
在Rt△BOD中,BD=$\sqrt{O{B}^{2}+O{D}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
故答案为$\sqrt{13}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理和平行线的性质.解决本题的关键是证明△OBD为直角三角形.

练习册系列答案
相关题目
20.一组数据:-2,-1,0,2,-1,1,则这组数据的众数为( )
| A. | 1 | B. | -1 | C. | 2 | D. | 0 |