题目内容
求三个不同的正整数a,b,c使
+
+
=
,且使[a,b,c]最小.
| 11 |
| a |
| 11 |
| b |
| 11 |
| c |
| 143 |
| 210 |
考点:整数问题的综合运用
专题:
分析:首先把原式化简为:
+
+
=
,210=2×3×5×7,要使[a,b,c]最小,则a,b,c的最大公约数要最大,且尽量为倍数关系,且剩余的质因数和质因数积的和小于13,由此探讨得出答案即可.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 13 |
| 210 |
解答:解:∵
+
+
=
,
∴
+
+
=
,
∵210=2×3×5×7,
∴要使[a,b,c]最小,则a,b,c的最大公约数要最大,且尽量为倍数关系,
当(a,b,c)=6
则13=1+5+7,则a,b,c分别为30,42,210,[a,b,c]=210;
当(a,b,c)=10
则13=3+3+7,不合题意;
当(a,b,c)=14
则13=3+5+5,不合题意;
当(a,b,c)=15
则13=2+4+7,则a,b,c分别为105,30,52.5,不合题意;
当(a,b,c)=21
则13=1+2+10或2+5+6,a,b,c分别为210,105,21或105,42,35,则[a,b,c]=210;
当(a,b,c)=35
则13=3+2+8,a,b,c分别为70,105,26.25不合题意;
综上所述,[a,b,c]最小为210.
| 11 |
| a |
| 11 |
| b |
| 11 |
| c |
| 143 |
| 210 |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 13 |
| 210 |
∵210=2×3×5×7,
∴要使[a,b,c]最小,则a,b,c的最大公约数要最大,且尽量为倍数关系,
当(a,b,c)=6
则13=1+5+7,则a,b,c分别为30,42,210,[a,b,c]=210;
当(a,b,c)=10
则13=3+3+7,不合题意;
当(a,b,c)=14
则13=3+5+5,不合题意;
当(a,b,c)=15
则13=2+4+7,则a,b,c分别为105,30,52.5,不合题意;
当(a,b,c)=21
则13=1+2+10或2+5+6,a,b,c分别为210,105,21或105,42,35,则[a,b,c]=210;
当(a,b,c)=35
则13=3+2+8,a,b,c分别为70,105,26.25不合题意;
综上所述,[a,b,c]最小为210.
点评:此题考查整数的分解质因数和最大公约数、最小公倍数的综合运用,注意抓住式子的特点,选用适当的方法解答即可.

练习册系列答案
相关题目
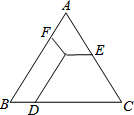 如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够,不能确定 |
计算:2-3=( )
| A、5 | B、1 | C、-5 | D、-1 |
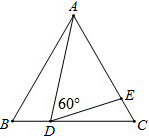 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为 如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD.
如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD. 如图,已知直线
如图,已知直线