题目内容
3.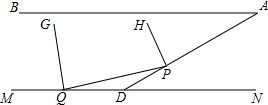 如图,∠BAD=35°,过D作MN∥AB,P是线段AD上的点,Q在射线DM上,射线QG平分∠PQM,射线PH平分∠APQ,PF∥QG,请补全图形,求$\frac{∠HPF}{∠ADN}$的值.
如图,∠BAD=35°,过D作MN∥AB,P是线段AD上的点,Q在射线DM上,射线QG平分∠PQM,射线PH平分∠APQ,PF∥QG,请补全图形,求$\frac{∠HPF}{∠ADN}$的值.
分析 利用平行线的性质得出∠ADN=35°,∠GQP+∠FPQ=180°,再利用角平分线的性质以及三角形外角的性质得出∠GQP+∠HPQ=$\frac{360°-35°}{2}$=162.5°,进而求出即可.
解答  解:如图所示:∵MN∥AB,∠BAD=35°,
解:如图所示:∵MN∥AB,∠BAD=35°,
∴∠ADN=35°,
∵射线QG平分∠PGM,射线PH平分∠APQ,
∴∠GQP+∠HPQ=$\frac{360°-35°}{2}$=162.5°,
∵PF∥QG,
∴∠GQP+∠FPQ=180°,
∴∠FPH=17.5°,
∴$\frac{∠HPF}{∠ADN}$=$\frac{1}{2}$.
点评 此题主要考查了平行线的性质以及角平分线的性质和三角形外角的性质等知识,得出∠GQP+∠HPQ的度数是解题关键.

练习册系列答案
相关题目
15.|-2|的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
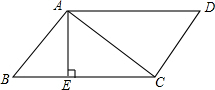 如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.
如图,在?ABCD中,AE⊥BC,垂足为E,且E为BC中点,若?ABCD的周长为20cm,△ABC的周长比?ABCD的周长少6cm,求?ABCD各边的长.