题目内容
14.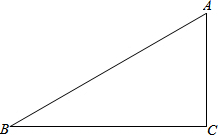 如图,在△ABC中,AB=17,BC=15,AC=8.
如图,在△ABC中,AB=17,BC=15,AC=8.(1)按以下要求进行尺规作图:
①作△ABC的内切圆O,连接AO并延长交BC于D;
②过O作OE⊥BC于E;
(2)猜想∠BOD与∠COE的大小关系,并证明.
分析 (1)作∠BAC和∠ACB的角平分线,它们相交于点O,作OE⊥BC于E,然后以点O为圆心,OE为半径作⊙O即可;
(2)先利用勾股定理的逆定理得到△ABC为直角三角形,∠ACB=90°,再根据三角形内心的性质得∠OCE=∠OCA,∠OBA=∠OBD,∠OAB=∠OAC,则∠OCE=$\frac{1}{2}$∠ACB=45°,易得∠COE=45°,再利用三角形外角性质可计算出∠BOD=∠OBA+∠OAB=$\frac{1}{2}$(∠ABC+∠BAC)=45°,于是有∠BOD=∠COE.
解答 解:(1)如图,⊙O为△ABC的内切圆;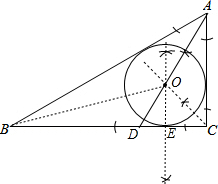
(2)∠BOD=∠COE.理由如下:
∵AB=17,BC=15,AC=8,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°,
∵⊙O为△ABC的内切圆,
∴∠OCE=∠OCA,∠OBA=∠OBD,∠OAB=∠OAC,
∴∠OCE=45°,
∵OE⊥BC,
∴∠COE=45°,
∵∠BOD=∠OBA+∠OAB=$\frac{1}{2}$(∠ABC+∠BAC)=$\frac{1}{2}$(180°-∠ACB)=45°,
∴∠BOD=∠COE.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的内切圆与内心.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图,若在一张边长为40cm的正方形硬纸板的四周剪掉两个矩形和两个正方形,将剩余部分折成一个有盖的长方体盒子,若折成的长方体盒子的表面积为1350cm2,求此时长方体盒子的长、宽、高.
如图,若在一张边长为40cm的正方形硬纸板的四周剪掉两个矩形和两个正方形,将剩余部分折成一个有盖的长方体盒子,若折成的长方体盒子的表面积为1350cm2,求此时长方体盒子的长、宽、高.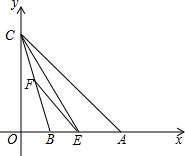 如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.
如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.