题目内容
11.把抛物线y=x2沿直线y=x向上平移2$\sqrt{2}$个单位后,则平移后的抛物线解析式是y=x2-4x+6.分析 沿直线y=x向上平移2$\sqrt{2}$个单位,即向右平移2个单位长度,向上平移2个单位长度,利用平移法则即可求解.
解答 解:沿直线y=x向上平移2$\sqrt{2}$个单位,即向右平移2个单位长度,向上平移2个单位长度.
则抛物线y=x2沿y=x向上平移2$\sqrt{2}$个单位后抛物线解析式是y=(x-2)2+2.即y=x2-4x+6.
故答案是:y=x2-4x+6.
点评 此题考查了二次函数图象的平移与几何变换,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.当a=$\sqrt{2}$,b=1时,代数式(a+2b)(a-2b)的值为( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
19. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )| A. | ∠1=∠2 | B. | ∠1+∠2=90° | C. | ∠1+∠2=180° | D. | 不能确定 |
6.已知抛物线y=ax2+bx+c(a<b<0)与x轴最多有一个交点,现有以下结论:
①c<0;②该抛物线的对称轴在y轴左侧;③关于x的方程ax2+bx+c+2=0有实数根;④对于自变量x的任意一个取值,都有$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$,其中正确的为( )
①c<0;②该抛物线的对称轴在y轴左侧;③关于x的方程ax2+bx+c+2=0有实数根;④对于自变量x的任意一个取值,都有$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$,其中正确的为( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
1.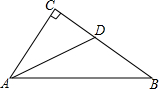 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
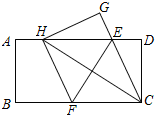 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: