题目内容
6.已知抛物线y=ax2+bx+c(a<b<0)与x轴最多有一个交点,现有以下结论:①c<0;②该抛物线的对称轴在y轴左侧;③关于x的方程ax2+bx+c+2=0有实数根;④对于自变量x的任意一个取值,都有$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$,其中正确的为( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
分析 从抛物线与x轴最多一个交点及a<b<0,可以推断抛物线有最大值为0,对称轴在y轴左侧,并得到b2-4ac≤0,从而得到①②为正确,③错误;利用函数y=函数y=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,根据函数的最值问题即可解决.④正确.
解答 解:∵a<b<0
∴-$\frac{b}{2a}$<0,抛物线有最大值为0,
∴c<0;该抛物线的对称轴在y轴左侧;
所以①正确;②正确;
∵抛物线与x轴最多有一个交点,
∴b2-4ac≤0,
∴关于x的方程ax2+bx+c+2=0中,△=b2-4a(c+2)=b2-4ac-8a,
∵a<0,
∴-8a>0,
当|b2-4ac|≥|8a|,则关于x的方程ax2+bx+c+2=0有实数根,
当|b2-4ac|<|8a|,则关于x的方程ax2+bx+c+2=0无实数根,
∴关于x的方程ax2+bx+c+2=0的根的情况不确定;
所以③错误;
∵函数y=$\frac{a}{b}$x2+x=$\frac{a}{b}$(x2+$\frac{b}{a}$x)=$\frac{a}{b}$(x+$\frac{b}{2a}$)2-$\frac{b}{4a}$,
∵$\frac{a}{b}$>0,
∴函数y有最小值-$\frac{b}{4a}$,
∴$\frac{a}{b}$x2+x≥-$\frac{b}{4a}$.所以④正确.
故选:B.
点评 本题考查了二次函数的解析式与图象的关系,解答此题的关键是要明确a的符号决定了抛物线开口方向;a、b的符号决定对称轴的位置;抛物线与x轴的交点个数,决定了b2-4ac的符号.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案| A. | 在1和2之间 | B. | 在2和3之间 | C. | 在3和4之间 | D. | 在4和5之间 |
| A. | 方程 3x-2=2x+1,移项,得 3x-2x=-1+2 | |
| B. | 方程 3-x=2-5(x-1),去括号,得 3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}$x=$\frac{3}{2}$,未知数系数化为 1,得 x=1 | |
| D. | 方程$\frac{x-1}{2}$-$\frac{x}{5}$=1 化成 5(x-1)-2x=10 |
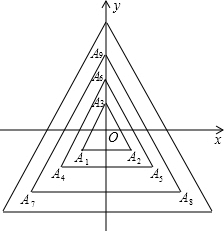 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673). 己知在梯形ABCD中,AB∥DC,∠A=∠B=45°,AB=4,AD=$\sqrt{2}$,则此梯形的面积是3.
己知在梯形ABCD中,AB∥DC,∠A=∠B=45°,AB=4,AD=$\sqrt{2}$,则此梯形的面积是3.