题目内容
3.求方程组$\left\{\begin{array}{l}{x+y+z=3}\\{{x}^{3}+{y}^{3}+{z}^{3}=3}\end{array}\right.$的所有整数解.分析 原方程组化为x+y=3-z③和x3+y3=3-z3④,由③④得出xy=$\frac{8-9z+3{z}^{2}}{3-z}$⑥,把x,y看成是以下二次方程的两个整数根:t2-(3-z)t+$\frac{8-9z+3{z}^{2}}{3-z}$=0,用求根公式解方程,再判断△为整数时,z为整数时的可能,进而得出对应的整数x,y.
解答 解:$\left\{\begin{array}{l}{x+y+z=3①}\\{{x}^{3}+{y}^{3}+{z}^{3}=3②}\end{array}\right.$,
①化为:x+y=3-z③,
②化为:x3+y3=3-z3④
③3-④,化简得,xy(x+y)=8-9z+3z2⑤
①代入⑤,可化简得,xy=$\frac{8-9z+3{z}^{2}}{3-z}$⑥,
由③、⑥知,x、y是以下二次方程的两个整数根:t2-(3-z)t+$\frac{8-9z+3{z}^{2}}{3-z}$=0,
∴t=$\frac{(3-z)±\sqrt{(3-z)^{2}-4×\frac{8-9z+3{z}^{2}}{3-z}}}{2}$
而△=$(3-z)^{2}-4×\frac{8-9z+3z2}{3-z}=(z-1)^{2}×\frac{z+5}{z-3}$=(z-1)2×(1+$\frac{8}{z-3}$)
∵x,y,z是整数,
∴t是整数,
∴(z-1)2×(1+$\frac{8}{z-3}$)是整数,
∴Ⅰ、当z-1=0时,即:z=1时,x=y=1;
Ⅱ、当z-3=1时,即:z=4时,x=4,y=-5或x=-5,y=4;
Ⅲ、当z-3=-8时,即:z=-5时,x=y=4,
∴方程组$\left\{\begin{array}{l}{x+y+z=3}\\{{x}^{3}+{y}^{3}+{z}^{3}=3}\end{array}\right.$的所有整数解有四组,$\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=1}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=4}\\{y=-5}\\{z=4}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=-5}\\{y=4}\\{z=4}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=4}\\{y=4}\\{z=-5}\end{array}\right.$.
点评 此题是非不定一次不定方程组,主要考查了一元二次方程的解法,满足整数解得条件,解本题的关键是将x,y作为一个一元二次方程的整数解,难点是△的化简处理,计算量比较大,是一道难度比较大的竞赛题.

| A. | ±4 | B. | ±2 | C. | 4 | D. | 2 |
| A. | $\sqrt{27}$÷$\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
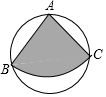 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )| A. | 4-$\frac{π}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
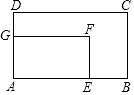 如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )
如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )| A. | $\sqrt{13}$ | B. | 2$\sqrt{13}$ | C. | 3$\sqrt{13}$ | D. | 12 |
| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=2 | D. | 直线x=-2 |
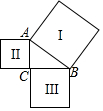 如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( ) 如图,在△ABC中,AB=10,AD平分∠BAC交BC于点D,若AD=8,BD=6,求AC的长.
如图,在△ABC中,AB=10,AD平分∠BAC交BC于点D,若AD=8,BD=6,求AC的长.