题目内容
19.下列图案属于轴对称图形的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析.
解答 解:A、不是轴对称图形,故此选项错误;
B、不是轴对称图形,故此选项错误;
C、不是轴对称图形,故此选项错误;
D、是轴对称图形,故此选项正确;
故选:D.
点评 此题主要考查了轴对称图形,关键是正确确定对称轴位置.

练习册系列答案
相关题目
9.下列选项中,能使关于x的一元二次方程ax2-4x+c=0一定有实数根的是( )
| A. | a>0 | B. | a=0 | C. | c<0 | D. | c=0 |
10.已知⊙O的半径为1,点A到圆心O的距离为a,若关于x的方程x2-2x+a=0不存在实数根,则点A与⊙O的位置关系是( )
| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O内 | D. | 无法确定 |
7. 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
14.下面计算正确的是( )
| A. | $\sqrt{27}$÷$\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
4.若$\sqrt{2x-y}$+|y+2|=0,则(xy)2的值是|( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
8.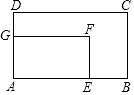 如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )
如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )
 如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )
如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为$\frac{2}{3}$,则C、F之间的距离为( )| A. | $\sqrt{13}$ | B. | 2$\sqrt{13}$ | C. | 3$\sqrt{13}$ | D. | 12 |
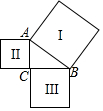 如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )
如图,以Rt△ABC的三边为边分别作正方形Ⅰ、Ⅱ、Ⅲ,已知正方形Ⅰ与正方形Ⅱ的面积分别为25和9,则正方形Ⅲ的面积为( )