题目内容
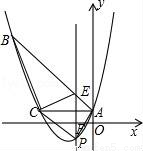
4. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
分析 过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,根据线段垂直平分线求出DE=BD=x,根据等腰三角形求出BD=DC=6,求出CM=DM=3,解直角三角形求出EM=3y,AQ=6y,在Rt△DEM中,根据勾股定理求出即可.
解答 解: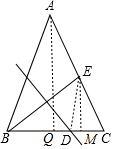
过A作AQ⊥BC于Q,过E作EM⊥BC于M,连接DE,
∵BE的垂直平分线交BC于D,BD=x,
∴BD=DE=x,
∵AB=AC,BC=12,tan∠ACB=y,
∴$\frac{EM}{MC}$=$\frac{AQ}{CQ}$=y,BQ=CQ=6,
∴AQ=6y,
∵AQ⊥BC,EM⊥BC,
∴AQ∥EM,
∵E为AC中点,
∴CM=QM=$\frac{1}{2}$CQ=3,
∴EM=3y,
∴DM=12-3-x=9-x,
在Rt△EDM中,由勾股定理得:x2=(3y)2+(9-x)2,
即2x-y2=9,
故选B.
点评 本题考查了线段垂直平分线性质,等腰三角形的性质,勾股定理,解直角三角形等知识点,能正确作出辅助线是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列实数中,无理数是( )
| A. | 2 | B. | 3.333 | C. | -π | D. | $\sqrt{4}$ |
15.从标有号数1到10的10张卡片中,随意抽取一张,其号数为3的倍数的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
12.计算(-1+2)×(-$\frac{1}{2}$)2÷(-2)的结果是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶点A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是13米,梯坎坡度i=1:2.4,则大楼AB的高度约为( )
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶点A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是13米,梯坎坡度i=1:2.4,则大楼AB的高度约为( )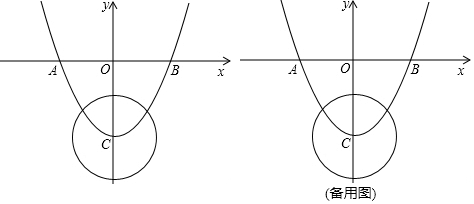
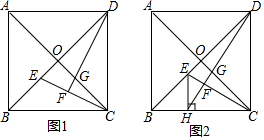
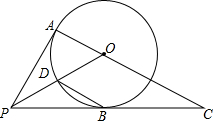 如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.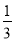 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.