题目内容
16. 如图,平移直线y=-x,平移后的直线与双曲线y=$\frac{1}{x}$(x>0)有唯一的公共点A与双曲线y=$\frac{k}{x}$(x<0)交于点B,与y轴交于点C,若y轴平分△AOB的面积,求k的值.
如图,平移直线y=-x,平移后的直线与双曲线y=$\frac{1}{x}$(x>0)有唯一的公共点A与双曲线y=$\frac{k}{x}$(x<0)交于点B,与y轴交于点C,若y轴平分△AOB的面积,求k的值.
分析 设平移后的直线解析式为:y=-x+b,根据一元二次方程根的判别式求出b的值,解方程组求出点A的坐标,根据题意确定点B的坐标,利用待定系数法求解即可.
解答 解:设平移后的直线解析式为:y=-x+b,
由题意得,方程组$\left\{\begin{array}{l}{y=-x+b}\\{y=\frac{1}{x}}\end{array}\right.$有一个公共解,
则x2-bx+1=0有两个相等的实数根,
则b2-4=0,
解得,b1=2,b2=-2(舍去),
解方程组$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{x}}\end{array}\right.$得,$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
则点A的坐标为(1,1),
∵y轴平分△AOB的面积,
∴BC=AC,
则点B的坐标为(-1,3),
∴3=$\frac{k}{-1}$,
解得,k=-3.
点评 本题考查了待定系数法求函数的解析式以及一元二次方程方程根的判别式的应用,求得A、B的坐标是解题的关键.

练习册系列答案
相关题目
15. 如图,数轴上点P对应的数为p,则数轴上与数-$\frac{p}{2}$对应的点是( )
如图,数轴上点P对应的数为p,则数轴上与数-$\frac{p}{2}$对应的点是( )
 如图,数轴上点P对应的数为p,则数轴上与数-$\frac{p}{2}$对应的点是( )
如图,数轴上点P对应的数为p,则数轴上与数-$\frac{p}{2}$对应的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
7.某衡器厂生产的RGZ-120型体重天平,最大称重120kg,你在体检时可看到显示盘,已知指针顺时针旋转角x(度)与体重y(kg)有如下关系:
(1)请写出y与x之间的函数表达式;
(2)当指针旋转到158.4度的位置时,求出此时的体重.
| x(度) | 0 | 72 | 144 | 216 | … |
| y(kg) | 0 | 25 | 50 | 75 | … |
(2)当指针旋转到158.4度的位置时,求出此时的体重.
5. 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )
 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
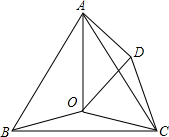 已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD.
已知:如图,O是等边△ABC内一点,∠AOB=105°,将△BOC绕点C顺时针旋转使CB与CA重合,得到△ADC,连接OD. 如图,∠POQ=45°,画△ABC关于OP对称的△A1B1C1,再画出△A1B1C1关于OQ对称△A2B2C2,△A2B2C2能否看作由△ABC旋转而得到的?如果能,找出旋转中心和旋转角度,如果不能,请说明理由.
如图,∠POQ=45°,画△ABC关于OP对称的△A1B1C1,再画出△A1B1C1关于OQ对称△A2B2C2,△A2B2C2能否看作由△ABC旋转而得到的?如果能,找出旋转中心和旋转角度,如果不能,请说明理由.
 已知△ABC中,AB=AC,∠BAC=45°,绕点C顺时针旋转△ABC,使点B落在AB边上,得△A1B1C(如图),联结AA1
已知△ABC中,AB=AC,∠BAC=45°,绕点C顺时针旋转△ABC,使点B落在AB边上,得△A1B1C(如图),联结AA1 如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标.
如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标.