题目内容
7.某衡器厂生产的RGZ-120型体重天平,最大称重120kg,你在体检时可看到显示盘,已知指针顺时针旋转角x(度)与体重y(kg)有如下关系:| x(度) | 0 | 72 | 144 | 216 | … |
| y(kg) | 0 | 25 | 50 | 75 | … |
(2)当指针旋转到158.4度的位置时,求出此时的体重.
分析 (1)根据给定的数据可以发现y与x之间的关系是一次函数关系,设y与x之间的函数表达式为y=kx+b(k≠0),根据点(0,0)、(72,25)利用待定系数法即可求出该一次函数的表达式,再根据最大称重120kg,即可得出x的取值范围;
(2)将x=158.4代入函数表达式中求出y值,此题得解.
解答 解:(1)观察表格数据,发现y与x之间的关系应为一次函数关系,设y与x之间的函数表达式为y=kx+b(k≠0),
将(0,0)、(72,25)代入y=kx+b中,
得:$\left\{\begin{array}{l}{b=0}\\{72k+b=25}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{25}{72}}\\{b=0}\end{array}\right.$,
∴y与x之间的函数表达式为y=$\frac{25}{72}$x.
令y=120,则有120=$\frac{25}{72}$x,
解得:x=345.6.
∴y与x之间的函数表达式为y=$\frac{25}{72}$x(0≤x≤345.6).
(2)当x=158.4时,y=$\frac{25}{72}$×158.4=55.
答:当指针旋转到158.4度的位置时,此时的体重为55千克.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,解题的关键是:(1)利用待定系数法求出函数关系式;(2)将x=158.4代入函数解析式中求出y值.本题属于中档题,难度不大,解决该题型题目时,得出函数关系式后结合给定条件,找出自变量的取值范围是关键.

练习册系列答案
相关题目
6.下列方程:
①x2-9=0;②(x+3)(x-1)=x2;③(2x+1)(2x-1)=0;④$\frac{1}{3x}$-y2=0;⑤x2=0.
其中是一元二次方程的个数是( )
①x2-9=0;②(x+3)(x-1)=x2;③(2x+1)(2x-1)=0;④$\frac{1}{3x}$-y2=0;⑤x2=0.
其中是一元二次方程的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
7.对于一般的二次函数y=x2+bx+c,经过配方可化为y=(x-1)2+2,则b,c的值分别为( )
| A. | 5,-1 | B. | 2,3 | C. | -2,3 | D. | -2,-3 |
4. 甲、乙两人都从A地出发,分别沿北偏东30°、60°的方向到达C地,且BC⊥AB,则B地在C地的( )
甲、乙两人都从A地出发,分别沿北偏东30°、60°的方向到达C地,且BC⊥AB,则B地在C地的( )
 甲、乙两人都从A地出发,分别沿北偏东30°、60°的方向到达C地,且BC⊥AB,则B地在C地的( )
甲、乙两人都从A地出发,分别沿北偏东30°、60°的方向到达C地,且BC⊥AB,则B地在C地的( )| A. | 北偏东30°的方向上 | B. | 北偏西30°的方向上 | ||
| C. | 南偏东30°的方向上 | D. | 南偏西30°的方向上 |
2.元旦到了,邮政部门与希望工程联合推出了一项业务,发行面值为3角和5角的明信片,所得收人捐赠贫困地区失学儿童,初三(1)班有23位同学,他们身上带有零用钱从8角到3元,钱数各不相同(每人带的钱都是以角为最小单位).他们为支持这项义举.把身上的零用钱全部购买明信片,又尽量多买3角一张的明信片(每人各自购买),则这23位同学所有购买的3角一张的明片最多可能是( )
| A. | 144张 | B. | 138张 | C. | 109张 | D. | 108张 |
17. 下列各图中,可以由图平移得到的是( )
下列各图中,可以由图平移得到的是( )
 下列各图中,可以由图平移得到的是( )
下列各图中,可以由图平移得到的是( )| A. |  | B. |  | C. |  | D. |  |




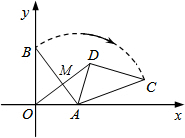 在平面直角坐标系中,已知点 A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,使点B在直线CD上,连接OD交AB于点M,直线CD的解析式为y=-$\frac{7}{24}$x+4.
在平面直角坐标系中,已知点 A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,使点B在直线CD上,连接OD交AB于点M,直线CD的解析式为y=-$\frac{7}{24}$x+4. 如图,平移直线y=-x,平移后的直线与双曲线y=$\frac{1}{x}$(x>0)有唯一的公共点A与双曲线y=$\frac{k}{x}$(x<0)交于点B,与y轴交于点C,若y轴平分△AOB的面积,求k的值.
如图,平移直线y=-x,平移后的直线与双曲线y=$\frac{1}{x}$(x>0)有唯一的公共点A与双曲线y=$\frac{k}{x}$(x<0)交于点B,与y轴交于点C,若y轴平分△AOB的面积,求k的值.