题目内容

13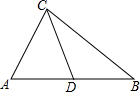．如图，△ABC中，点D在线段AB上，且△ABC∽△ACD，则下列结论一定正确的是（　　）
A．AC2=AB•ADB．AC2=BC•ADC．AC•CD=AB•ADD．AC•CD=CD•BD

分析 根据相似三角形对应边成比例列式整理即可得解．

解答 解：∵△ABC∽△ACD，
∴$\frac{AB}{AC}$=$\frac{AC}{AD}$=$\frac{BC}{CD}$，
∴AC2=AB•AD．
故选A．

点评 本题考查了相似三角形的性质，熟练掌握对应顶点的字母放在对应位置上并准确确定出对应边是解题的关键．

练习册系列答案
相关题目
18．我们学习了勾股定理后，都知道“勾三、股四、弦五”．
观察：3、4、5；5、12、13；7、24、25；9、40、41；…，发现这些勾股数的勾都是奇数，且从3起就没有间断过．
（1）请你根据上述的规律写出下一组勾股数：11，60，61；
（2）若第一个数用字母n（n为奇数，且n≥3）表示，那么后两个数用含n的代数式分别表示为$\frac{{{n^2}-1}}{2}$和$\frac{{{n^2}+1}}{2}$，请用所学知识说明它们是一组勾股数．
19．如图，已知AB∥CD，∠DFE=130°，则∠ABE的度数为（　　）
A．40°B．50°C．60°D．130°
1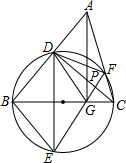．如图，在锐角△ABC中，以BC为直径的圆分别交AB，AC于点D，F．若E，D关于BC对称，连接EF交BC于点G，AG与CD相交于点P，则点P一定为△DFG的（　　）
A．外心B．内心C．垂心D．以上答案都不对
8．用配方法解方程x2+1=8x，变形后的结果正确的是（　　）
A．（x+4）2=15B．（x+4）2=17C．（x-4）2=15D．（x-4）2=17
18．解方程：（1-2x）2=x2-6x+9．
5．对于实数a，b，定义运算“*”：$a*b=\left\{\begin{array}{l}{a^2}-ab（a≥b）\\ ab-{a^2}（a＜b）\end{array}\right.$，例如，4*3，因为4＞3，所以4*3=42-4×3=4．若x1，x2是一元二次方程x2-8x+12=0的两个根，则x1*x2=8或24．
2．在等式y=ax+b中，当x=2时，y的值的-1，当x=$\frac{1}{2}$，y的值是2，则b=3．
3．数学课外兴趣小组的同学每人制作一个面积为200cm2的三角形学具进行展示．设三角形的一边长为xcm，该边上的高为ycm，那么这些同学所制作的三角形的高y（cm）与边长x（cm）之间的函数关系的图象大致是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网