题目内容
20．已知一次函数y=2x+b交x轴于点A（-2，0），交y轴于点B，则点B坐标为（0，4）．分析 由A点坐标可求得b的值，再令x=0可求得相应y的值，可求得B点坐标．
解答 解：∵一次函数y=2x+b交x轴于点A（-2，0），
∴0=-4+b，解得b=4，
∴一次函数解析式为y=2x+4，
令x=0，可得y=4，
∴B点坐标为（0，4），
故答案为：（0，4）．
点评 本题主要考查函数图象上点的坐标，掌握函数图象上的点的坐标满足函数解析式是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
11．
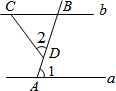如图，已知：直线a、b被AB所截，交点分别是点A、B，其中a∥b，∠1=72°，点D是线段AB上一点，CD=BD．则∠2=（ ）
如图，已知：直线a、b被AB所截，交点分别是点A、B，其中a∥b，∠1=72°，点D是线段AB上一点，CD=BD．则∠2=（ ）| A． | 72° | B． | 36° | C． | 64° | D． | 56° |
8．不论x取何值，抛物线y=ax2+bx+c都不与x轴相交，且顶点永远在x轴下方的条件是（ ）
| A． | a＞0，b2-4ac≥0 | B． | a＜0，b2-4ac≥0 | C． | a＞0，b2-4ac＜0 | D． | a＜0，b2-4ac＜0 |
15．
如图，AB∥CD，点E在BC上，且CD=CE，∠D=68°，则∠B的度数为（ ）
如图，AB∥CD，点E在BC上，且CD=CE，∠D=68°，则∠B的度数为（ ）| A． | 22° | B． | 32° | C． | 44° | D． | 68° |