题目内容
8．不论x取何值，抛物线y=ax2+bx+c都不与x轴相交，且顶点永远在x轴下方的条件是（ ）| A． | a＞0，b2-4ac≥0 | B． | a＜0，b2-4ac≥0 | C． | a＞0，b2-4ac＜0 | D． | a＜0，b2-4ac＜0 |
分析 由抛物线y=ax2+bx+c都不与x轴相交则可知b2-4ac＜0，由顶点永远在x轴下方可知抛物线的开口向下即a＜0，进而得到问题的答案．
解答 解：∵抛物线y=ax2+bx+c都不与x轴相交
∴b2-4ac＜0，
∵顶点永远在x轴下方
∴抛物线的开口向下，
即a＜0，
故选D．
点评 本题考查了抛物线和x轴交点的问题，难度一般．学生要熟记二次函数的性质方能得心应手的解题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．分式$\frac{{a}^{2}+a}{{a}^{2}+2a+1}$化简的结果是（ ）
| A． | $\frac{a}{a-1}$ | B． | $\frac{a+1}{a-1}$ | C． | $\frac{a}{a+1}$ | D． | a |
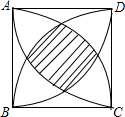如图，正方形ABCD的边长为a，分别以正方形的四个顶点为圆心，边长为半径，在正方形内画弧，求图中阴影部分的面积．
13．如果a＞b，下列各式中不正确的是（ ）
| A． | a-4＞b-4 | B． | -$\frac{a}{3}$＜-$\frac{b}{3}$ | C． | -2a＜-2b | D． | -5+a＜-5+b |