题目内容
10.若数a使关于x的分式方程$\frac{2}{x-1}$+$\frac{a}{1-x}$=4的解为正数,且使关于y的不等式组$\left\{\begin{array}{l}\frac{y+2}{3}-\frac{y}{2}>1\\ 2({y-a})≤0\end{array}$的解集为y<-2,则符合条件的所有整数a的和为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 根据分式方程的解为正数即可得出a<6且a≠2,根据不等式组的解集为y<-2,即可得出a≥-2,找出-2≤a<6且a≠2中所有的整数,将其相加即可得出结论.
解答 解:分式方程$\frac{2}{x-1}$+$\frac{a}{1-x}$=4的解为x=$\frac{6-a}{4}$且x≠1,
∵关于x的分式方程$\frac{2}{x-1}$+$\frac{a}{1-x}$=4的解为正数,
∴$\frac{6-a}{4}$>0且$\frac{6-a}{4}$≠1,
∴a<6且a≠2.
$\left\{\begin{array}{l}{\frac{y+2}{3}-\frac{y}{2}>1①}\\{2(y-a)≤0②}\end{array}\right.$,
解不等式①得:y<-2;
解不等式②得:y≤a.
∵关于y的不等式组$\left\{\begin{array}{l}\frac{y+2}{3}-\frac{y}{2}>1\\ 2({y-a})≤0\end{array}$的解集为y<-2,
∴a≥-2.
∴-2≤a<6且a≠2.
∵a为整数,
∴a=-2、-1、0、1、3、4、5,
(-2)+(-1)+0+1+3+4+5=10.
故选A.
点评 本题考查了分式方程的解以及解一元一次不等式,根据分式方程的解为正数结合不等式组的解集为y<-2,找出-2≤a<6且a≠2是解题的关键.

练习册系列答案
相关题目
5.要使分式$\frac{4}{x-3}$有意义,x应满足的条件是( )
| A. | x>3 | B. | x=3 | C. | x<3 | D. | x≠3 |
2.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则-3℃表示气温为( )
| A. | 零上3℃ | B. | 零下3℃ | C. | 零上7℃ | D. | 零下7℃ |
19.($\frac{1}{3}$)-2的相反数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
 小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.
小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.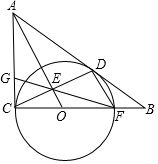 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.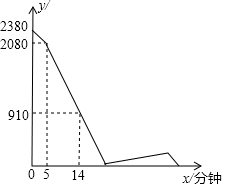 A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.
A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.