题目内容
10. 如图,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.若反比例函数y=$\frac{m}{x}$(x>0)的图象与线段AC有公共点,则m的取值范围为1≤m≤4.
如图,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.若反比例函数y=$\frac{m}{x}$(x>0)的图象与线段AC有公共点,则m的取值范围为1≤m≤4.
分析 根据题意得出C两点的坐标,把A点和C点坐标代入反比例函数y=$\frac{m}{x}$(x>0),求出m的值即可.
解答 解:∵Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3,
∴C(4,1),
当反比例函数y=$\frac{m}{x}$(x>0)的图象经过点A(1,1),
∴m=1;
当函数图象经过点C(4,1)时,m=4,
∴m的取值范围为:1≤m≤4,
故答案为:1≤m≤4.
点评 本题考查的是反比例函数的性质,熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键,学会灵活应用待定系数法,属于中考常考题型.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
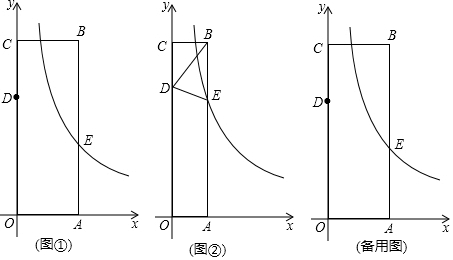
5. 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )| A. | 50米 | B. | 100米 | C. | 125米 | D. | 150米 |
15.方程x-1=5+2x的解为( )
| A. | .x=-2 | B. | x=2 | C. | x=-6 | D. | x=6 |
2.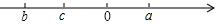 若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
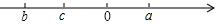 若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )
若有理数a、b、c在数轴上的位置如图所示,则下列正确的式子是( )| A. | a>b>c>0 | B. | c<b<0<a | C. | a>0>c>b | D. | c>b>0>a |
19.下列根式中,能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{30}$ |
20.在函数y=$\frac{\sqrt{3-x}}{x+2}$中,自变量x的取值范围是( )
| A. | x≤3且x≠-2 | B. | x≤3 | C. | x≠-2 | D. | x<3且x≠-2 |