题目内容
将多边形切去一角后得到的多边形的内角和为900°,则原多边形的边数为 .
考点:多边形内角与外角
专题:
分析:先根据多边形的内角和公式(n-2)•180°求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
解答:解:设多边形截去一个角的边数为n,
则(n-2)•180°=900°,
解得n=7,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是6或7或8.
故答案为:6或7或8.
则(n-2)•180°=900°,
解得n=7,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是6或7或8.
故答案为:6或7或8.
点评:本题考查了多边形的内角和公式,本题难点在于多边形截去一个角后边数有增加1,不变,减少1三种情况.

练习册系列答案
相关题目
二次函数y=-3x2+12的图象与坐标轴的交点个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )
若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )| A、1个 | B、2个 | C、3个 | D、4个 |
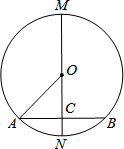 如图,⊙O的直径MN垂直弦AB于点C,若OM=5cm.下列结论中可能成立的是( )
如图,⊙O的直径MN垂直弦AB于点C,若OM=5cm.下列结论中可能成立的是( )| A、AB=12cm |
| B、OC=6cm |
| C、MN=8cm |
| D、AC=2.5cm |
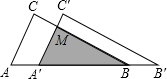 如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=
如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=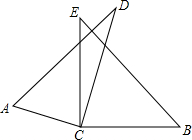 如图,将两块直角三角尺的直角顶点C叠放在一起
如图,将两块直角三角尺的直角顶点C叠放在一起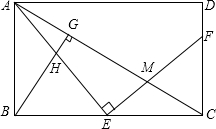 如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.