题目内容
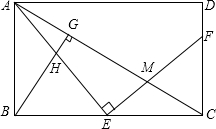 如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=3,求EM的长.
考点:相似三角形的判定与性质,矩形的性质
专题:
分析:(1)如图,首先证明∠BAE=∠CEF,结合∠ABE=∠ECF=90°,即可解决问题.
(2)△ABH∽△ECM.首先证明∠ABH=∠ECM;运用∠BAH=∠CEM,即可解决问题.
(3)如图,作辅助线;证明△ABC∽△MRC,结合AB=BE=EC=3,证明∠AEB=45°,得到∠MER=45°,CR=2MR;求出MR=ER=1,即可解决问题.
(2)△ABH∽△ECM.首先证明∠ABH=∠ECM;运用∠BAH=∠CEM,即可解决问题.
(3)如图,作辅助线;证明△ABC∽△MRC,结合AB=BE=EC=3,证明∠AEB=45°,得到∠MER=45°,CR=2MR;求出MR=ER=1,即可解决问题.
解答: (1)证明:如图,∵四边形ABCD是矩形,
(1)证明:如图,∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°;
∵AE⊥EF,∠AEB+∠FEC=90°,
∴∠AEB+∠BEA=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF.
(2)△ABH∽△ECM.证明如下:
证明:∵BG⊥AC,∠ABC=90°,
∴∠ABG+∠BAG=90°,∠ECM+∠BAG=90°,
∴∠ABH=∠ECM;
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM.
(3)解:作MR⊥BC,垂足为R,
则△ABC∽△MRC,而AB=BE=EC=3,
∴AB:BC=MR:RC=1:2,∠AEB=45°,
∴∠MER=45°,CR=2MR;
∵ER+RC=EC=3
∴MR=ER=1
∴EM=
=
.
 (1)证明:如图,∵四边形ABCD是矩形,
(1)证明:如图,∵四边形ABCD是矩形,∴∠ABE=∠ECF=90°;
∵AE⊥EF,∠AEB+∠FEC=90°,
∴∠AEB+∠BEA=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF.
(2)△ABH∽△ECM.证明如下:
证明:∵BG⊥AC,∠ABC=90°,
∴∠ABG+∠BAG=90°,∠ECM+∠BAG=90°,
∴∠ABH=∠ECM;
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM.
(3)解:作MR⊥BC,垂足为R,
则△ABC∽△MRC,而AB=BE=EC=3,
∴AB:BC=MR:RC=1:2,∠AEB=45°,
∴∠MER=45°,CR=2MR;
∵ER+RC=EC=3
∴MR=ER=1
∴EM=
| 12+12 |
| 2 |
点评:该题主要考查了矩形的性质、相似三角形的判定及其性质等几何知识点及其应用问题;应牢固掌握矩形的性质、相似三角形的判定及其性质,这是灵活运用解题的基础和工具.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )
如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )| A、10° | B、20° |
| C、7.5° | D、15° |
 如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,王玲同学根据给定的条件写出了四个结论:①AP⊥BP;②点P到AD,BC的距离相等;③PD=PC;④AD+BC=AB,其中结论正确的个数有( )
如图,已知AD∥BC,AP平分∠DAB,BP平分∠ABC,点P恰好在CD上,王玲同学根据给定的条件写出了四个结论:①AP⊥BP;②点P到AD,BC的距离相等;③PD=PC;④AD+BC=AB,其中结论正确的个数有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )| A、3 | ||||
B、3
| ||||
C、
| ||||
D、
|
 Rt△ABC中AB是斜边,AC=BC,点P是△ABC内一点,将△APC绕C逆时针旋转后能与△BDC完全重合,若PC=5,则PD的值是多少?
Rt△ABC中AB是斜边,AC=BC,点P是△ABC内一点,将△APC绕C逆时针旋转后能与△BDC完全重合,若PC=5,则PD的值是多少?
 如图,已知△ABC.
如图,已知△ABC.