题目内容
8. 如图,EB是直径,O是圆心,CB,CD切半圆于B,D,CD交BE延长线于点A,若BC=6,AD=2AE,求半圆的面积.
如图,EB是直径,O是圆心,CB,CD切半圆于B,D,CD交BE延长线于点A,若BC=6,AD=2AE,求半圆的面积.
分析 连接DE、BD,根据切线的性质得出DC=BC=6,∠ADE=∠ABD,证得△ADE∽△ABD,根据相似三角形的性质得出AB=2AD,设AD=x,则AB=2x,AC=AD+DC=x+6,然后根据勾股定理得出关于x的方程,求得AD的长,即可求得AE和AB,从而求得直径,根据圆的面积公式求得即可.
解答  解:连接DE、BD,
解:连接DE、BD,
∵CB,CD切半圆于B,D,
∴DC=BC=6,
∴∠ADE=∠ABD,
∵∠DAE=∠BAD,
∴△ADE∽△ABD,
∴$\frac{AE}{AD}$=$\frac{AD}{AB}$,
∵AD=2AE,
∴$\frac{AD}{AB}$=$\frac{1}{2}$,
∴AB=2AD,
设AD=x,则AB=2x,
∴AC=AD+DC=x+6,
∵CB切半圆于B,EB是直径,
∴AB⊥BC,
∴AC2=AB2+BC2,即(x+6)2=(2x)2+62,
解得x1=4,x2=0(舍去),
∴AE=2,AB=8,
∴BE=AB-AE=8-2=6,
∴圆的半径为3,
∴半圆的面积=$\frac{1}{2}$π×32=$\frac{9}{2}$π.
点评 本题考查了切线的性质,三角形相似的判定和性质,勾股定理的应用,作出辅助线,构建相似三角形是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
6.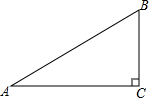 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,c=10,则下列不正确的是( )| A. | ∠B=60° | B. | a=5 | C. | b=5$\sqrt{3}$ | D. | tanB=$\frac{\sqrt{3}}{3}$ |
18.若分式$\frac{a+1}{a-1}$有意义,则( )
| A. | a≠1 | B. | a=1 | C. | a≠1或-1 | D. | a=1或-1 |
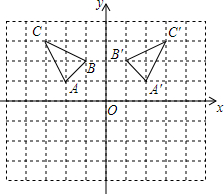 如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
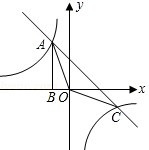 如图,Rt△ABO的顶点A是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.