题目内容
 如图,在平面直角坐标系中,点0为坐标原点,A点在x轴正半轴上,B点在第一象限内,AO=5,∠AOB=30°,∠BAO=60°.
如图,在平面直角坐标系中,点0为坐标原点,A点在x轴正半轴上,B点在第一象限内,AO=5,∠AOB=30°,∠BAO=60°.(1)求B点的坐标;
(2)求直线AB的解析式.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)作BC⊥x轴于C,如图,设BC=t,根据含30度的直角三角形三边的关系,在Rt△OBC中,计算出OC=
BC=
t,在Rt△ACB中,计算出AC=
BC=
t,由于OA=5,则
t+
t=5,解得t=
,所以OC=
t=
,于是得到B点坐标为(
,
);
(2)利用待定系数法求直线AB的解析式.
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
5
| ||
| 4 |
| 3 |
| 15 |
| 4 |
| 15 |
| 4 |
5
| ||
| 4 |
(2)利用待定系数法求直线AB的解析式.
解答: 解:(1)作BC⊥x轴于C,如图,
解:(1)作BC⊥x轴于C,如图,
设BC=t,
在Rt△OBC中,∠AOB=30°,
∴OC=
BC=
t,
在Rt△ACB中,∠BAO=60°,
∴AC=
BC=
t,
∵OA=5,
∴
t+
t=5,解得t=
,
∴OC=
t=
∴B点坐标为(
,
);
(2)设直线AB的解析式为y=kx+b,
把A(5,0)、B(
,
)代入得
,解得
,
所以直线AB的解析式为y=-
x+5
.
 解:(1)作BC⊥x轴于C,如图,
解:(1)作BC⊥x轴于C,如图,设BC=t,
在Rt△OBC中,∠AOB=30°,
∴OC=
| 3 |
| 3 |
在Rt△ACB中,∠BAO=60°,
∴AC=
| ||
| 3 |
| ||
| 3 |
∵OA=5,
∴
| 3 |
| ||
| 3 |
5
| ||
| 4 |
∴OC=
| 3 |
| 15 |
| 4 |
∴B点坐标为(
| 15 |
| 4 |
5
| ||
| 4 |
(2)设直线AB的解析式为y=kx+b,
把A(5,0)、B(
| 15 |
| 4 |
5
| ||
| 4 |
|
|
所以直线AB的解析式为y=-
| 3 |
| 3 |
点评:本题考查了两直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
要锻造一个半径为5厘米,高为8厘米的圆柱毛坯,应截取半径为4厘米的圆钢( )
| A、12.5cm |
| B、13cm |
| C、13.5cm |
| D、14cm |
 如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由. 小明和爷爷一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,爷爷先跑.当小明出发时,爷爷已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
小明和爷爷一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,爷爷先跑.当小明出发时,爷爷已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题: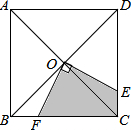 如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.
如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.
