题目内容
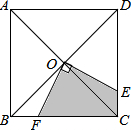 如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.
如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.(1)OE与OF相等吗?若相等请说明理由;
(2)若AC=10cm,求阴影四边形的面积.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据ASA证明△OBF≌△OCE,再根据全等三角形的性质即可得到OE与OF相等;
(2)根据割补法得到阴影四边形的面积等于△BOC的面积,根据三角形面积公式即可求解.
(2)根据割补法得到阴影四边形的面积等于△BOC的面积,根据三角形面积公式即可求解.
解答:解:(1)∵正方形ABCD的对角线AC、BD的交点为O,
∴BO=CO,∠BOC=90°,∠OBF=∠OCE=45°,
∵∠EOF=90°,
∴∠BOF=∠COE,
在△OBF与△OCE中,
,
∴△OBF≌△OCE(ASA),
∴OE=OF,
(2)∵△OBF≌△OCE,
∴阴影四边形的面积=△BOC的面积=
×(10÷2)×(10÷2)=12.5cm2.
∴BO=CO,∠BOC=90°,∠OBF=∠OCE=45°,
∵∠EOF=90°,
∴∠BOF=∠COE,
在△OBF与△OCE中,
|
∴△OBF≌△OCE(ASA),
∴OE=OF,
(2)∵△OBF≌△OCE,
∴阴影四边形的面积=△BOC的面积=
| 1 |
| 2 |
点评:考查了正方形的性质和全等三角形的判定与性质,以及三角形面积减少,本题关键是得到△OBF≌△OCE.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目


 如图,已知△ABC中,AB=AC=20cm,BC=16cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=20cm,BC=16cm,点D为AB的中点. 如图,在平面直角坐标系中,点0为坐标原点,A点在x轴正半轴上,B点在第一象限内,AO=5,∠AOB=30°,∠BAO=60°.
如图,在平面直角坐标系中,点0为坐标原点,A点在x轴正半轴上,B点在第一象限内,AO=5,∠AOB=30°,∠BAO=60°.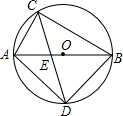 如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长.
如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.
在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.