题目内容
5．若一个等腰直角三角形的面积为8，则这个等腰三角形的直角边长为（ ）| A． | 2$\sqrt{2}$ | B． | 4$\sqrt{2}$ | C． | 4 | D． | 8 |
分析 设等腰直角三角形的直角边长为x，根据面积为8，可列方程求解．
解答 解；设等腰直角三角形的直角边长为x，
则$\frac{1}{2}$x2=8，
x=4或x=-4（舍去）．
所以它的直角边长为4．
故选C．
点评 本题考查等腰直角三角形的性质，等腰直角三角形的两个腰相等，两腰夹角为90°，根据面积为8可列方程求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．
如图，已知点D是△ABC的重心，若AE=4，则AC的长度为（ ）
如图，已知点D是△ABC的重心，若AE=4，则AC的长度为（ ）| A． | 4 | B． | 8 | C． | 10 | D． | 12 |
16．下列反比例函数中，图象经过点（1，-1）的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=$\frac{-1}{x}$ | C． | y=$\frac{2}{x}$ | D． | y=$\frac{-2}{x}$ |
暑假就要来了，小明为自己制定了慢跑锻炼计划，某日小明从家出发沿解放路慢跑，已知他离家的距离s（千米）与时间t（分钟）之间的关系如图所示，请根据图象直接回答下列问题：
20．菱形两条对角线长为6和8，菱形的边长为a，面积为S，则下列正确的是（ ）
| A． | a=5，S=24 | B． | a=5，S=48 | C． | a=6，S=24 | D． | a=8，S=48 |
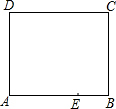如图是一张长方形纸片ABCD，若AB=8，AD=6，E为AB上的一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$．
19．-|-sin60°|的值是（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $-\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |