题目内容
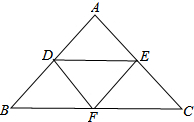 已知D、E、F分别为△ABC的AB、AC、BC边上的中点,求证:S△DEF=
已知D、E、F分别为△ABC的AB、AC、BC边上的中点,求证:S△DEF=| 1 |
| 4 |
考点:三角形中位线定理,相似三角形的判定与性质
专题:
分析:首先证明四边形ABCD是平行四边形,可得DE=FB,再根据三角形的面积公式可得S△DFE=S△DBF,同理可得S△EFC=S△ADE=S△DEF,进而得到S△DEF=
S△ABC.
| 1 |
| 4 |
解答: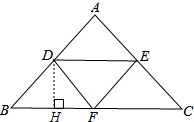 证明:过D作DH⊥BC,
证明:过D作DH⊥BC,
∵D、E分别为△ABC的AB、AC边上的中点,
∴DE∥BF,DE=
BC,
∵F是BC中点,
∴FB=
BC,
∴DE=BF,
∴四边形ABCD是平行四边形,
∴DE=FB,
∵S△BDF=
FB•DH,S△DEF=
ED•DH,
∴S△DFE=S△DBF,
同理:S△EFC=S△ADE=S△DEF,
∴S△DEF=
S△ABC.
 证明:过D作DH⊥BC,
证明:过D作DH⊥BC,∵D、E分别为△ABC的AB、AC边上的中点,
∴DE∥BF,DE=
| 1 |
| 2 |
∵F是BC中点,
∴FB=
| 1 |
| 2 |
∴DE=BF,
∴四边形ABCD是平行四边形,
∴DE=FB,
∵S△BDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DFE=S△DBF,
同理:S△EFC=S△ADE=S△DEF,
∴S△DEF=
| 1 |
| 4 |
点评:此题主要考查了三角形的中位线,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
若a<0,b<0,则下列各式一定成立的是( )
| A、a-b<0 |
| B、a-b>0 |
| C、a-b=0 |
| D、-a-b>0 |