题目内容
16．
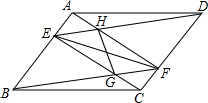如图，在平行四边形ABCD中，点E、F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H、G．求证：（1）四边形AECF是平行四边形．
（2）EF与GH互相平分．
分析 （1）由平行四边形的性质得出AB∥CD，AB=CD，由AE=CF，即可得出结论；
（2）由平行四边形的性质得出AF∥CE，再证明四边形BFDE是平行四边形，得出BF∥DE，证出四边形EGFH是平行四边形，即可得出结论．
解答 证明：（1）∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵AE=CF，
∴四边形AECF是平行四边形．
（2）由（1）得：四边形AECF是平行四边形，
∴AF∥CE，
∵AE=CF，AB∥CD，AB=CD，
∴BE∥DF，BE=DF，
∴四边形BFDE是平行四边形，
∴BF∥DE，
∴四边形EGFH是平行四边形，
∴EF与GH互相平分．
点评 本题考查了平行四边形的判定与性质；熟记一组对边平行且相等的四边形是平行四边形，证明四边形是平行四边形是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中，AB=AC，∠A=36°，BD平分∠ABC．求证：$\frac{BC}{AB}=\frac{\sqrt{5}-1}{2}$．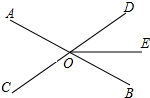
如图，直线AB、CD相交于点O，OE平分∠BOD，若∠AOD=2∠DOB，则∠EOB=30°．