题目内容
8. 如图,在△ABC中,AB=AC,点D为BC上一点,点G为AD上一点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:∠1=∠2.
如图,在△ABC中,AB=AC,点D为BC上一点,点G为AD上一点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF,求证:∠1=∠2.
分析 先证明△ABO≌△ACO(SAS),得到∠ABO=∠ACO,由AB=AC,得到∠ABC=∠ACB,所以∠ABC-∠ABO=∠ACB-∠ACO,即∠1=∠2.
解答 解:∵DE⊥AB于点E,DF⊥AC于点F,且DE=DF,
∴AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABO和△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$
∴△ABO≌△ACO(SAS),
∴∠ABO=∠ACO,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠ABO=∠ACB-∠ACO,
即∠1=∠2.
点评 本题考查了全等三角形的性质与判定、等腰三角形的性质,解决本题的关键是证明△ABO≌△ACO(SAS),得到∠ABO=∠ACO.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
3. 如图所示,在数轴上有六个点,且AB=BC=CD=DE=EF,则点C表示的数是( )
如图所示,在数轴上有六个点,且AB=BC=CD=DE=EF,则点C表示的数是( )
 如图所示,在数轴上有六个点,且AB=BC=CD=DE=EF,则点C表示的数是( )
如图所示,在数轴上有六个点,且AB=BC=CD=DE=EF,则点C表示的数是( )| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
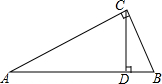 如图所示,CD是Rt△ABC的斜边AB上的高.
如图所示,CD是Rt△ABC的斜边AB上的高.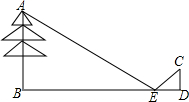 如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米.
如图所示,在距树18米的地面上平放一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰巧看见树顶,若人眼C距地面1.4米.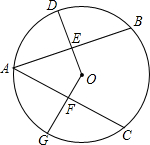 如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF.
如图,AB=AC,D为$\widehat{AB}$的中点,G为$\widehat{AC}$的中点,求证:DE=GF. 如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.
如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.