题目内容
18．已知y=x+1，求$\frac{{x}^{2}-2xy{+y}^{2}}{2x+y}$÷（1-$\frac{x+2y}{2x+y}$）的值．分析 根据分式的混合运算顺序和法则先化简原式，再由y=x+1得x-y=-1即可得出分式的值．
解答 解：原式=$\frac{（x-y）^{2}}{2x+y}$÷$\frac{2x+y-x-2y}{2x+y}$
=$\frac{（x-y）^{2}}{2x+y}$•$\frac{2x+y}{x-y}$
=x-y，
∵y=x+1，
∴x-y=-1，
∴原式=-1．
点评 本题主要考查分式的化简求值，熟练掌握分式的混合运算顺序和法则是解题的关键．
练习册系列答案
相关题目
9．
如图所示，该几何体的俯视图是（ ）
如图所示，该几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
3．
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛，在安全知识竞赛结束后，赛后发现所有参赛学生会的成绩都高于50分．为了了解本次大赛的成绩分布情况，某校随机抽取了其中200名学生的成绩（成绩x取整数，总分为100分）作为样本进行统计分析，得到如下不完整的统计图表，请根据图标中的信息解答下列各题：
（1）频数分布表中a=60，b=0.05；本次比赛成绩的中位数会落在80≤x＜90分数段；
（2）请补全频数分布直方图；
（3）该校安全知识竞赛成绩满分（100分）共有4人，其中男生2名，女生2名，为了激励学生增强安全意识，现需要从这4人中随机抽取2人介绍学习经验，请用“列表法”或“画树状图”，求恰好选到一男一女的概率．
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛，在安全知识竞赛结束后，赛后发现所有参赛学生会的成绩都高于50分．为了了解本次大赛的成绩分布情况，某校随机抽取了其中200名学生的成绩（成绩x取整数，总分为100分）作为样本进行统计分析，得到如下不完整的统计图表，请根据图标中的信息解答下列各题：| 成绩（分） | 频数 | 频数 |
| 50＜x≤60 | 10 | b |
| 60＜x≤70 | 20 | 0.10 |
| 70＜x≤80 | 30 | 0.15 |
| 80＜x≤90 | a | 0.30 |
| 90＜x≤100 | 80 | 0.40 |
（2）请补全频数分布直方图；
（3）该校安全知识竞赛成绩满分（100分）共有4人，其中男生2名，女生2名，为了激励学生增强安全意识，现需要从这4人中随机抽取2人介绍学习经验，请用“列表法”或“画树状图”，求恰好选到一男一女的概率．
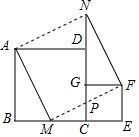如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM=b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD=∠AND；②CP=b-$\frac{{b}^{2}}{a}$；③△ABM≌△NGF；④S四边形AMFN=a2+b2；⑤A，M，P，D四点共圆，其中正确的个数是（ ）
8．“五一”期间，某市共接待海内外游客约567000人次，将567000用科学记数法表示为（ ）
| A． | 567×103 | B． | 56.7×104 | C． | 5.67×105 | D． | 0.567×106 |