题目内容
9.已知关于x的方程组$\left\{\begin{array}{l}{3x+y=k-1}\\{4x+3y=k+1}\end{array}\right.$的解满足2x-y>-1.(1)求k的取值范围;
(2)若n是(1)中的k的最小整数,且满足2x+5y-n=0,则4x-1•32y的值为2.
分析 (1)根据解方程组,联系条件,利用整体直接进行计算(若不能直接看出式子与条件的联系可以用待定系数法求每个式子的系数),再根据解不等式,可得k的范围;
(2)根据n的值,可得(2x+5y),根据幂的乘方底数不变指数相乘,可得同底数幂的乘法,根据同底数幂的乘法底数不变指数相加,可得负整数指数幂,根据负整数指数幂,可得答案.
解答 解:(1)关于x的方程组$\left\{\begin{array}{l}{3x+y=k-1①}\\{4x+3y=k+1②}\end{array}\right.$,
①×2-②得:2x-y=k-3
又2x-y>-1,所以k-3>-1,解得:k>2.
(2)n是(1)中的k的最小整数,得
n=3.故2x+5y=3;
又4x-1•32y=22x-2•25y=22x+5y-2=21=2,
故答案为:2.
点评 本题考查了二元一次方程组的解,利用方程组的解得出不等式是解题关键;利用幂的乘方得出同底数幂的乘法是解题关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
17.下列各式中是分式的是( )
| A. | $\frac{{a}^{2}}{3}$ | B. | $\frac{x-y}{2}$ | C. | $\frac{1}{x+y}$ | D. | $\frac{2016}{π}$ |
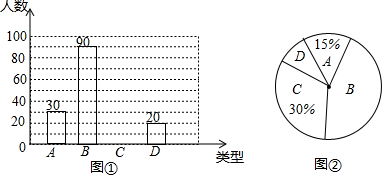
4.小芳连续5天测得最低气温并整理后得出下表,
由于不小心被墨迹污染了两个数据,这两个数据分别是4,$\sqrt{2}$.
| 日期 | 一 | 二 | 三 | 四 | 五 | 标准差 | 平均气温 |
| 最低气温(℃) | 1 | 3 | 2 | 5 |  |  | 3 |
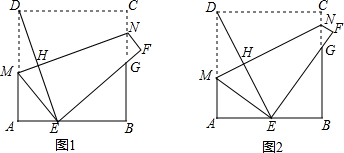
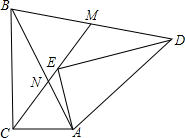 如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.
如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.