题目内容
已知线段AB和CD的公共部分BD=
AB=
CD,线段AB、CD的中点E、F之间的距离是14cm,求BD和AC的长.
| 1 |
| 4 |
| 1 |
| 5 |
考点:两点间的距离
专题:计算题
分析:如图,设BD=x,则AB=4x,CD=5x,根据线段中点的定义得AE=BE=2x,DF=CF=2.5x,则DE=BE-BD=x,EF=DE+DF=3.5x,于是可得到方程3.5x=14,解得x=4,则BD=4,然后利用AC=AE+DE+CD=8x计算AC的长.
解答:解:如图, 设BD=x,则AB=4x,CD=5x,
设BD=x,则AB=4x,CD=5x,
∵E、F分别为线段AB、CD的中点,
∴AE=BE=
AB=2x,DF=CF=
CD=2.5x,
∴DE=BE-BD=2x-x=x,
∴EF=DE+DF=x+2.5x=3.5x,即3.5x=14,解得x=4,
∴BD=4,
AC=AE+DE+CD=2x+x+5x=8x=32.
 设BD=x,则AB=4x,CD=5x,
设BD=x,则AB=4x,CD=5x,∵E、F分别为线段AB、CD的中点,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=BE-BD=2x-x=x,
∴EF=DE+DF=x+2.5x=3.5x,即3.5x=14,解得x=4,
∴BD=4,
AC=AE+DE+CD=2x+x+5x=8x=32.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.注意强调最后的两个字“长度”,也就是说,距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.常用代数式计算距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折?
如图,将一张三角形纸片ABC(如图)折叠,点A落在A′处,若要使折痕DE∥BC,则应怎么折?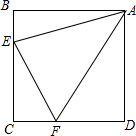 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.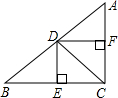 如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F.
如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,过点D分别作DE⊥BC,DF⊥AC,垂足分别为E,F. 如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.
如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.
